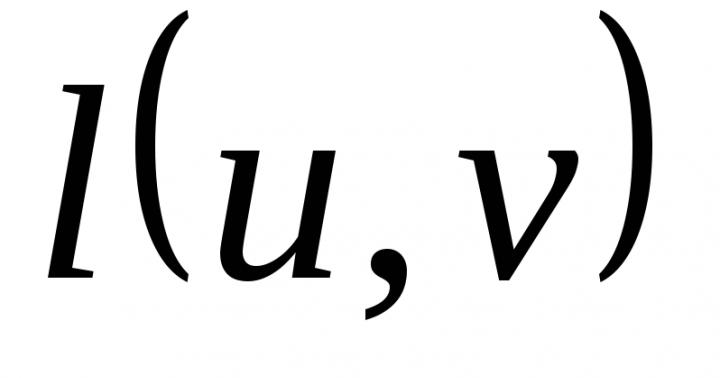Rozwiąż zadanie znalezienia najkrótszej ścieżki algorytmu DaEkstra.
Znajdź najkrótszą ścieżkę z X0 do X7. Liczba jest ustawiana przez elementy matrycy kosztów
Zbuduj ten wykres 
Zacznijmy od elementu X0 i przypisujemy go znacznik 0, uważaj wszystkich swoich sąsiadów, ponieważ Nadal nie ma uwagi, przypisujesz im odpowiednie długości: 
Wszyscy sąsiedzi X0 są brane pod uwagę, zaznaczamy go i idzie na górę X1. Sąsiedzi X0, X2, X4, ale X0 oznaczone, nie uważają tego. Dla x2: ![]() , Zostaw etykietę.
, Zostaw etykietę.
Dla x4: ![]() Wymiana etykiety. Wszyscy sąsiedzi Vertex X1 są brane pod uwagę, zaznaczamy to
Wymiana etykiety. Wszyscy sąsiedzi Vertex X1 są brane pod uwagę, zaznaczamy to 
Idź na górę x2. Sąsiedzi X0, X1, X3, X4, X5, X6, ale x0, X1 są oznaczone, nie uważaj ich.
Dla x3: ![]() , Zostaw etykietę.
, Zostaw etykietę.
Dla x5: ![]() Wymiana etykiety.
Wymiana etykiety.
Dla x4: ![]() , Zostaw etykietę.
, Zostaw etykietę.
Dla x6: ![]() Wymiana etykiety.
Wymiana etykiety.
Uważamy, że wszyscy sąsiedzi górnej części X2, zaznaczamy to. 
Idź do góry X3. Jego sąsiedzi x0, x2, x6, ale x0, x2 są oznaczone, nie uważają ich.
Dla x6: ![]() , Zostaw etykietę.
, Zostaw etykietę.
Wszyscy sąsiedzi szczytu X3 są brane pod uwagę, zaznaczamy to. 
Idź na górę x4. Jego sąsiedzi x1, x2, x5, x7, ale x1, x2 są zaznaczone, nie uważaj ich.
Dla x5: ![]() Wymiana etykiety.
Wymiana etykiety.
Dla x7: ![]() Wymiana etykiety.
Wymiana etykiety.
Wszyscy sąsiedzi szczytu X4 są brane pod uwagę, zaznaczamy to. 
Idź na górę X5. Jego sąsiedzi x2, x4, x6, x7, ale x2, x4 są zaznaczone, nie uważaj ich.
Dla x6: ![]() , Zostaw etykietę.
, Zostaw etykietę.
Dla x7: ![]() , Zostaw etykietę.
, Zostaw etykietę.
Wszyscy sąsiedzi szczytu X5 są brane pod uwagę, zaznaczamy to. 
Idź na górę x6. Jego sąsiedzi x2, x3, x5, x7, ale x2, x3, x5 są zaznaczone, nie uważaj ich.
Dla x7: ![]() , Zostaw etykietę.
, Zostaw etykietę.
Rozważane są wszystkie blaty X6, zaznaczamy to. I oznaczaliśmy pozostałe X7, wszystkie wierzchołki są brane pod uwagę. 
Wniosek: Najkrótsza ścieżka ich X0 w X7 ma długość 101, ta ścieżka: X7-X4-X1-X0.
Algorytm Daekstra (angielski algorytm Dijkstra) jest algorytmem na wykresach, wymyślonych przez Holandia Naukowiec Edsgera Dikstroja w 1959 roku. Znajduje najkrótsze ścieżki z jednego z wierzchołków wykresu do wszystkich innych. Algorytm pracuje tylko dla wykresów bez masy ujemnej wornadzkowej.
Rozważ realizację algorytmu na przykładzie wykresu pokazanego na rysunku.
Niech musi znaleźć najkrótszą odległość od pierwszego wierzchołka do wszystkich innych.
Okręgi wskazują wierzchołki, linie - ścieżka między nimi (liczyć na RIBR). W kółkach zaznaczył liczbę wierzchołków, na krawędziach są wskazywane przez ich "cenę" - długość ścieżki. Obok każdego szczytu czerwieni oznaczał etykietę - długość najkrótszej ścieżki do tego wierzchołka wierzchołka 1.
Pierwszy krok. Rozważysz etap algorytmu Deiquistry dla naszego przykładu. Minimalna etykieta ma wierzchołek 1. Sąsiedzi to wierzchołki 2, 3 i 6.
Pierwszy z kolei wierzchołków wierzchołka 1 - Top 2, ponieważ długość ścieżki jest minimalna. Długość ścieżki do niej przez wierzchołek 1 jest równa sumie wartości znacznika wierzchołka 1 i długości krawędzi pochodzącej z pierwszego do 2, czyli 0 + 7 \u003d 7. Jest Mniej niż bieżący znacznik wierzchołka 2, nieskończoność, więc nowa etykieta jest 2 wierzchołki są 7.
Podobne działanie odbywa się z dwoma innymi sąsiadami pierwszego wierzchołka - 3 i 6..
Wszystkie szczyty wierzchołka 1 są sprawdzane. Obecna minimalna odległość od wierzchołka 1 jest uważana za ostateczny, a wersja nie podlega (co naprawdę sprawdziła E. Dyakstra po raz pierwszy). Przekroczyłem go z wykresu, aby pamiętać, że ten górny jest odwiedzany.
Drugi krok. Krok algorytmu jest powtarzany. Znów znajdziemy "najbliższe" z nieświadomiej wierzchołków. Jest to wierzchołek 2 Tagged 7.
Spróbuj ponownie, aby zmniejszyć znaki sąsiadów wybranego wierzchołka, próbując wejść do nich przez drugi wierzchołek. Sąsiedzi wierzchołków 2 są wierzchołkami 1, 3 i 4.
Pierwszy (w porządku) sąsiadem wierzchołka 2 jest wierzchołek 1. Ale jest już odwiedzany, więc nic nie robimy z pierwszym wierzchołkiem.
Następnym sąsiadem wierzchołka 2 jest wierzchołek 3, ponieważ ma minimalny znacznik z wierzchołków oznaczonych, jak nie jest odwiedzany. Jeśli pójdziesz do niego w 2, to długość takiej ścieżki będzie równa 17 (7 + 10 \u003d 17). Ale obecny znak trzeciego wierzchołka wynosi 9, a to jest mniejsze niż 17, więc etykieta nie zmienia się.
Innym sąsiadem wierzchołka 2 jest wierzchołek 4. Jeśli przejdziesz do niego przez drugą, to długość takiej ścieżki będzie równa sumie najkrótszej odległości do drugiego wierzchołka i odległość między wierzchołkami 2 i 4 , to znaczy 22 (7 + 15 \u003d 22). Od 22.<, устанавливаем метку вершины 4 равной 22.
Wszystkie szczyty wierzchołka 2 są oglądane, zamrozić odległość do niego i zaznaczamy go jako odwiedzane.
Trzeci krok. Powtarzamy etap algorytmu, wybierając wierzchołek 3. Po jego "przetwarzaniu" otrzymujemy wyniki:
Dalsze kroki. Powtarzamy krok algorytmu do pozostałych wierzchołków. Będą one odpowiednio wierzchołków 6, 4 i 5, zamów.
Zakończenie wykonania algorytmu. Algorytm kończy pracę, gdy nie można przetwarzać żadnego wierzchołka. W tym przykładzie wszystkie wierzchołki są utopione, ale pomyli się, by wierzyć, że to tak w żadnym przykładzie - niektóre wierzchołki mogą pozostać niezwiązane, jeśli nie można go zdobyć, tj. Jeśli liczba jest niejednoznaczna. Wynik algorytmu jest widoczny na ostatnim rysunku: Najkrótsza ścieżka z wierzchołka 1 do drugiego wynosi 7, do 3-9, do 4 - 20, do 5 do 20, do 6 - 11.
Wdrożenie algorytmu w różnych językach programowania:
C ++.
#Include "stdafx.h" #includePascal.
Program Dijkstraalgoritm; Używa CRT; const v \u003d 6; inf \u003d 100000; Wpisz Vektor \u003d tablica całkowitego; Var Start: Integer; Const Gr: Array of Intereger \u003d ((((((((((0, 1, 4, 0, 2, 0), (0, 0, 0, 9, 0, 0), (4, 0, 0, 7, 0, 0), (0, 9, 7, 0, 0, 2), (0, 0, 0, 0, 0, 8), (0, 0, 0, 0, 0, 0)); (Algorytm Dikstra) Procedura Dijkstra (GR: Tablica całkowita; St: Integer); Var Count, indeks, I, U, M, Min: Integer; Odległość: Vektor; Odwiedzone: tablica Boolean; Rozpocznij m: \u003d st; Dla I: \u003d 1 do V Rozpocznij odległość [I]: \u003d inf; Odwiedził [i]: \u003d false; koniec; Odległość: \u003d 0; Do liczby: \u003d 1 do V-1 rozpocznij Min: \u003d Inf; Dla I: \u003d 1 do V Do jeśli (nie odwiedzaj [i]) i (odległość [i]<=min) then begin min:=distance[i]; index:=i; end; u:=index; visited[u]:=true; for i:=1 to V do if (not visited[i]) and (GR<>0) i (odległość [U]<>inf) i (odległość [U] + grJawa.
Importuj java.io.bufferedreader; Importuj java.io.ioException; Import java.io.InputStreamReader; Importuj java.io.printWriter; Importuj java.util.arraylist; Importuj java.util.arrays; Importuj java.util.stringTokedizer; Rozwiązanie klasy publicznej (prywatny statyczny INF \u003d INTEGER.MAX_VALUE / 2; Prywatny Int N; // Liczba wierzchołków w ORGRAPH Int M; // Liczba łuków W ORGRAPH Private ArraylistInna opcja:
Importuj Java.io. *; Importuj java.util. *; Klasa publiczna Dijkstra (Prywatny statyczny końcowy wykres. Regapt.Eved Graph \u003d (nowy wykres. Regument ("A", "B", 7), nowa grafika. Nowożeńcy "A", "F", 14), nowy wykres.EGE ("B", "C", 10), nowy wykres. Nege ("B", "D", 15), nowy wykres. Regulamin ("C "," D ", 11), nowa grafika. Regument (" C "," F ", 2), nowa grafika. Nowo-" D "," E ", 6), nowa grafika (" E ", "F", 9),); Prywatny statyczny końcowy ciąg START \u003d "A"; Prywatny statyczny końcowy koniec końcowy \u003d "e"; publiczne statyczne void Główne (String Args) (Wykres G \u003d Nowy wykres); G.dijkstra (Start ); G.printpath; //g.printallpaths ();)) Wykres klasy (prywatna mapa końcowa
DO.
#Zawierać.PHP.
$ Edge, "Koszt" \u003d\u003e $ Edge); $ sąsiedzi [$ Edge] \u003d tablica ("koniec" \u003d\u003e $ Edge, "Koszt" \u003d\u003e $ Edge); ) $ vertices \u003d array_Unique ($ wierzchołków); foreach ($ wierzchołki jako $ Vertex) ($ Div [Vertux] \u003d inf; $ poprzednie [Vertex] \u003d NULL;) $ Div [$ Source] \u003d 0; $ Q \u003d $ wierzchołków; While (Count ($ Q)\u003e 0) (// Todo - znajdź szybszy sposób uzyskania minimum $ min \u003d inf; foreach ($ q jako $ Vertex) (jeśli ($ Diste [$ Vetex]< $min) { $min = $dist[$vertex]; $u = $vertex; } } $Q = array_diff($Q, array($u)); if ($dist[$u] == INF or $u == $target) { break; } if (isset($neighbours[$u])) { foreach ($neighbours[$u] as $arr) { $alt = $dist[$u] + $arr["cost"]; if ($alt < $dist[$arr["end"]]) { $dist[$arr["end"]] = $alt; $previous[$arr["end"]] = $u; } } } } $path = array(); $u = $target; while (isset($previous[$u])) { array_unshift($path, $u); $u = $previous[$u]; } array_unshift($path, $u); return $path; } $graph_array = array(array("a", "b", 7), array("a", "c", 9), array("a", "f", 14), array("b", "c", 10), array("b", "d", 15), array("c", "d", 11), array("c", "f", 2), array("d", "e", 6), array("e", "f", 9)); $path = dijkstra($graph_array, "a", "e"); echo "path is: ".implode(", ", $path)."\n";
Pyton
Z kolekcji Import Namedtuple, kolejka z PPRINT Import PPRINT jako PP INF \u003d Float ("Edge", "Start, End, Koszt" Wykres klasy (): Def __init __ (Jaźń, Krawędzie): Self. Dramiges \u003d krawędzie2 \u003d Self. Wierzchołki \u003d zestaw (suma (dla E w krawędziach2),)) DEF Dijkstra (Self, źródło, DEST): Asert Źródło w self.vertics dist \u003d (wierzchołek: inF dla wierzchołka w self.vertics) Poprzedni \u003d (wierzchołek: brak dla wierzchołek w self.verticttics) dist \u003d 0 q \u003d self.vertics.copy () sąsiedzi \u003d (wierzchołek: zestaw () dla wierzchołka w self.d.verticals) na początek, koniec, koszt w samochodzie. Krawędzie: sąsieks.add ((koniec , Koszt)) #pp (sąsiedzi), podczas gdy q: u \u003d min (q, klawisz \u003d lambda wierzchołek: dist) Q.Remove (U), jeśli dist [u] \u003d\u003d inf lub u \u003d \u003d dest: przerwa na V, koszt w sąsiedzi [U]: alt \u003d dist [u] + koszt, jeśli alt< dist[v]: # Relax (u,v,a)
dist[v] = alt
previous[v] = u
#pp(previous)
s, u = deque(), dest
while previous[u]:
s.pushleft(u)
u = previous[u]
s.pushleft(u)
return s
graph = Graph([("a", "b", 7), ("a", "c", 9), ("a", "f", 14), ("b", "c", 10),
("b", "d", 15), ("c", "d", 11), ("c", "f", 2), ("d", "e", 6),
("e", "f", 9)])
pp(graph.dijkstra("a", "e"))
Output:
["a", "c", "d", "e"]
Wielu algorytmów wyszukiwania najkrótszych tras w kolumnie, w Habré, znalazłem opis algorytmu Floyd Warshlla. Ten algorytm znajduje najkrótszą ścieżkę między wszystkimi wierzchołkami wykresu i ich długości. W tym artykule opiszę zasadę działania algorytmu DaEkstra, który znajduje optymalne trasy i ich długość między jednym konkretnym wierzchołkiem (źródłem) a wszystkimi innymi wierzchołkami wykresu. Wadą tego algorytmu jest to, że nieprawidłowo działa, jeśli wykres ma ujemny łuk wagowy.
Na przykład, weź taką zorientowaną liczbę G:
Możemy sobie wyobrazić ten wykres w formie macierzy z:

Weź wierzchołek 1. Oznacza to, że poszukujemy najkrótszych tras z góry 1 do wierzchołków 2, 3, 4 i 5.
Ten algorytm krok po kroku przechodzi przez wszystkie wierzchołki wykresu i przypisuje im etykiety, które są znaną minimalną odległością od górnej części źródła do określonego wierzchołka. Rozważ ten algorytm na przykładzie.
Przypisujemy pierwszą górę etykiety równej 0, ponieważ ten wierzchołek jest źródłem. Reszta wierzchołków przypisuje znaczniki równe nieskończoności.

Następnie wybierz taki wierzchołek W, który ma minimalną wytwórnię (teraz jest wierzchołkiem 1) i rozważ wszystkie wierzchołki, do których z Vertex W jest ścieżką, która nie zawiera wierzchołków. Każdy z uważanych wierzchołków przypisujemy etykietę równą sumie znakowanej w i długości ścieżki z W do rozważanego wierzchołka, ale tylko wtedy, gdy wynikowa kwota jest mniejsza niż poprzednia wartość znacznika. Jeśli kwota nie jest mniejsza, pozostawiamy poprzednie etykietę niezmienioną.

Po uznaniu wszystkich wierzchołków, w których istnieje prosta ścieżka z W, wierzchołek W zaznaczamy zarówno odwiedzanych, jak i wybieramy nie odwiedzane, że ma minimalną wartość znacznika, będzie następujący wierzchołek W. w tym przypadku, Jest to wierzchołek 2 lub 5. Jeśli istnieje kilka wierzchołków z tymi samymi tagami, nie ma znaczenia, które wybieramy jako W.
Wybędziemy wierzchołek 2. Ale nie ma z niego pojedyncza ścieżka wychodząca, więc natychmiast świętujemy ten wierzchołek, jak odwiedziliśmy i przejdź do następnego wierzchołka z minimalną etykietą. Tym razem tylko wierzchołek 5 ma minimalną etykietę. Rozważ wszystkie wierzchołki, w których występują bezpośrednie ścieżki z 5, ale które nie są jeszcze oznaczone jako odwiedzane. Ponownie znajdziemy sumę szczytu wierzchołka W i ciężar żeber z W do bieżącego wierzchołka, a jeśli ta ilość jest mniejsza niż poprzednia tag, zastępujemy wartość etykiety do uzyskanej kwoty.

W oparciu o obraz, widzimy, że etykiety 3 i 4 wierzchołków były mniejsze niż, tj. Znaleziono krótszą drogę do tych wierzchołków z górnej części źródła. Następnie odnotowujemy 5th Vertex, jak odwiedził i wybierz następny wierzchołek, który ma minimalną etykietę. Powtarzamy wszystkie powyższe kroki, dopóki nie zostanie niewiastowane szczyty.
Po wykonaniu wszystkich działań otrzymujemy ten wynik:

Na podstawie którego można zbudować najkrótsze trasy. W przypadku liczby elementów, wektor ten jest równy liczbie wierzchołków w kolumnie, każdy element zawiera ostatni pośredni wierzchołek na najkrótszej ścieżce między górnym źródłem a końcowym wierzchołkiem. Na początku algorytmu wszystkie elementy wektora p są równe górnej części źródła (w naszym przypadku p \u003d (1, 1, 1, 1, 1)). Następnie, na etapie przeliczania wartość etykiety w rozważanym wierzchołku, jeśli w rozważanym znaczniku zmienia się na mniejszy, w tablicy R, piszą wartość bieżącego wierzchołka W. na przykład: 3rd Vertex miał etykietę o wartości "30", gdy W \u003d 1. Następnie, gdy W \u003d 5 znacznik 3 - zmienił się na "20", dlatego będziemy napisać wartość w wektorze p - p \u003d 5. Ponadto, gdy W \u003d 5 wartość etykiety zmieniła się w czwartym wierzchołku (była "50", stała się "40"), oznacza to, że musisz przypisać 4 element wektora p \u003d 5. W rezultacie otrzymujemy wektor p \u003d (1, 1, 5, 5, 1).
Wiedząc, że w każdym elemencie wektora P nagrał ostatni pośredni wierzchołek na drodze między źródłem a ostatecznym wierzchołkiem, możemy uzyskać najkrótszą trasę.
najkrótsza droga Dziś jest to ważne zadanie i jest używany niemal wszędzie, od znalezienia optymalnej trasy między dwoma obiektami na ziemi (na przykład najkrótszej ścieżki z domu na uniwersytet), w systemach autopilot, aby znaleźć optymalną trasę podczas transportu, Pakiet informacyjny w sieciach i T.P.Najkrótsza ścieżka jest uważana za pomocą pewnego obiektu matematycznego o nazwie wykres. Szukaj najkrótsza droga Jest prowadzony między dwoma określonymi wierzchołkami na wykresie. Rezultatem jest ścieżka, która jest sekwencją wierzchołków i żeber, incydent do dwóch sąsiednich wierzchołków i jej długości.
Rozważ trzy najwięcej skuteczny algorytm Nośny najkrótsza droga:
- algorytm Daekstra.;
- Algorytm Floyda;
- overnorn algorytmy.
Te algorytmy są łatwo wykonywane z małą liczbą wierzchołków na wykresie. Ze wzrostem ich liczby zadań wyszukiwania najkrótsza droga Kompletny.
Algorytm Daekstra.
Ten algorytm jest algorytmem na wykresach, który został wymyślony przez Holandia Naukowiec E. DyAKStroy w 1959 roku. Algorytm znajduje najkrótszą odległość od jednego z wierzchołków wykresu do wszystkich innych i działa tylko na wykresy bez żeber o negatywnej masy.
Każdy wierzchołek przypisuje się wagi - jest to waga ścieżki z początkowego wierzchołka do tego. Również każdy wierzchołek może być podświetlony. Jeśli wierzchołek jest podświetlony, ścieżka z niego do początkowego wierzchołka najkrótsza, jeśli nie, a następnie tymczasowa. Nadchodząc przez wykres, algorytm uważa drogę dla każdego wierzchołka, a jeśli okaże się najkrótszy, podkreśla górę. Waga tego wierzchołka jest ciężarem ścieżki. Dla wszystkich sąsiadów tego wierzchołka algorytm oblicza również wagę, bez żadnych okoliczności w żadnych okolicznościach. Algorytm kończy swoją pracę, osiągając ostateczny wierzchołek i ważenie najkrótsza droga Waga końcowego wierzchołka staje się.
Algorytm Daekstra.
Krok 1. Do wszystkich szczytów, z wyjątkiem pierwszego, waga przypisana jest równa nieskończoność, a pierwszy wierzchołek wynosi 0.
Krok 2. Wszystkie wierzchołki nie są podświetlone.
Krok 3. Pierwszy wierzchołek jest zadeklarowany prąd.
Krok 4. Waga wszystkich niezamieszkanych wierzchołków jest tłumaczona przez wzór: Masa niezbadanego wierzchołka jest minimalną liczbą starej masy tego wierzchołka, ilość masy prądu wierzchołka i masy krawędzi łączącej Aktualny wierzchołek z nierozróżnianym.
Krok 5. Wśród niezbędnych pików jest góra z minimalną wagą. Jeśli nie zostanie znalezione, to znaczy waga wszystkich wierzchołków jest równa nieskończoności, trasa nie istnieje. W konsekwencji wyjście. W przeciwnym razie prąd jest wynikiem wynikowym. Jest przydzielony.
Krok 6. Jeśli bieżący wierzchołek okazuje się być ostatecznym, pojawia się ścieżka, a jego waga jest masą końcowego wierzchołka.
Krok 7. Przejdź do Krok 4.
W realizacji oprogramowania algorytm Daekstra. Będziemy skonstruować zestaw wierzchołków S, dla których najkrótsze ścieżki z początkowego wierzchołka są już znane. Przy każdym kroku do set s dodaje się ten sam wierzchołek, odległość od początkowego wierzchołka jest mniejsza niż dla innych pozostałych wierzchołków. W tym przypadku użyjemy tablicy D, w której długości są rejestrowane najkrótsze ścieżki Dla każdego wierzchołka. Gdy set S zawiera wszystkie wierzchołki wykresu, a następnie tablarek D zawiera długości najkrótsze ścieżki Z początkowego wierzchołka do każdego wierzchołka.
Oprócz określonych tablic, użyjemy matrycy C C, gdzie element C jest długości krawędzi (I, J), jeśli nie ma żebra, to jego długość jest oparta na równej nieskończonej, to znaczy więcej niż jakakolwiek rzeczywista długość żebra. Właściwie matryca C jest matryca żeglarska.w którym wszystkie elementy zerowe są zastępowane nieskończonością.
Aby określić samą
Po zakończeniu turnieju sylwestrowego, sponsor postanowił wysłać prezenty $ m $ zwycięskie prezenty pocztą. Znajomość liczby uczestników $ N $ i czas dostawy poczty między działami "Ukrpochta", znajdziesz, po tym, jak minimalny czas ostatnia zwycięzców otrzyma nagrodę.
Dane wejściowe.
Pierwsza linia zawiera numery $ $ $ $: liczba uczestników turnieju $ n $, liczba nagród sponsora $ M $ oraz liczbę znanych tymczasowych czasów dostawy między niektórymi biurami $ K $. W następnym wierszu liczba uczestników, którzy zostali wskazani, są wskazane.
Dalej przychodzi $ k $ rzędy o wartości 3 $ numery z informacjami o znanych czasach dostawy między niektórymi przedziałami w formacie: $ A $ B $ $ T $, gdzie $ A $ b $ b $ - numery komorówek, $ t $ (0 Leqslant T Leqslant 365) Czas dostawy poczty między nimi. W ostatniej linii znajduje się pojedynczy numer - liczba poczty, z której sponsor wyśle \u200b\u200bnagrody. Wiadomo, że 1 $ LEQSLANT N, M, A, B LEQSLANT 365 USD.
Wynik
Jeśli wszystkie nagrody są dostarczane do uczestników - wycofać się w pierwszej linii "Dobry sponsor!", A w przyszłym czasie, po czym ostatni z zwycięzców otrzyma nagrodę. Jeśli przynajmniej jeden z uczestników może uzyskać nagrodę - wycofanie się w jedynej linii "nie jest winą sponsora ...". Wyjście zwrotne bez cytatów.
Testy
| № | Dane wejściowe | Wynik |
| 1. | 3 2 2 2 3 1 2 3 2 3 4 1 |
Dobry sponsor! 7 |
| 2. | 5 1 4 5 1 3 2 2 3 3 4 2 5 4 5 6 1 |
Dobry sponsor! 16 |
| 3. | 7 2 6 1 3 1 3 2 2 4 32 4 5 94 3 1 0 6 2 4 7 2 3 7 |
Nie jest winą sponsora ... |
| 4. | 5 2 6 1 2 3 1 1 3 4 2 2 4 3 5 1 4 4 5 5 2 3 7 2 |
Dobry sponsor! 6 |