در قرن گذشته ، ایوان برنولی ، لئونارد اویلر و سپس ژان باتیست فوریه ابتدا نماینده توابع دوره ای با استفاده از سری های مثلثاتی بودند. این دیدگاه در دوره های دیگر با جزئیات کافی مطالعه شده است ، بنابراین ما فقط روابط و تعاریف اساسی را به خاطر می آوریم.

همانطور که در بالا ذکر شد ، هر عملکرد دوره ای تو (تی) که برای آن برابری u (t) = u (t + T) ، جایی که T = 1 / F = 2p / W ، می تواند توسط یک سری فوریه نشان داده شود:

هر اصطلاح از این سری را می توان با استفاده از فرمول کسینوس برای تفاوت بین دو زاویه گسترش داد و به صورت دو عبارت نمایش داد:

,

جایی که: A n = C n cosφ n ، B n = C n sinφ n ، بنابراین ، آ

شانس A n و در n با فرمول های اولر تعیین می شوند:

;
.

در n = 0 :

آ B 0 = 0.

شانس A n و در n ، میانگین مقادیر حاصلضرب تابع هستند تو (تی) و نوسانات هارمونیک با فرکانس nw در فاصله زمانی تی ... ما قبلاً (بخش 2.5) می دانیم که این توابع همبستگی متقابل هستند و میزان ارتباط آنها را تعیین می کنند. بنابراین ، ضرایب A n و B n سینوسوئید یا کسینوس با فرکانس را به ما نشان دهید nW موجود در این تابع تو (تی) قابل گسترش در سری فوریه

بنابراین ، ما می توانیم تابع دوره ای را نشان دهیم تو (تی) به عنوان مجموع ارتعاشات هارمونیک ، که در آن اعداد C n دامنه ها و اعداد هستند φ n - فاز. معمولاً در ادبیات طیف دامنه نامیده می شود و - طیف فازها اغلب فقط طیف دامنه ها در نظر گرفته می شود که به صورت خطوط واقع شده در نقاط به تصویر کشیده شده است nW در محور فرکانس و دارای ارتفاع مربوط به عدد C n ... با این حال ، باید به خاطر داشت که برای بدست آوردن یک تناظر یک به یک بین عملکرد زمانی تو (تی) و طیف آن ، استفاده از طیف دامنه و طیف فاز ضروری است. این را می توان از چنین مثال ساده ای دریافت. طیف دامنه سیگنالها اما کاملاً خواهد بود نوع متفاوتتوابع موقت

یک طیف گسسته می تواند نه تنها یک عملکرد دوره ای داشته باشد. به عنوان مثال ، سیگنال: دوره ای نیست ، اما دارای طیف گسسته ای است که از دو خط طیفی تشکیل شده است. همچنین ، یک سیگنال دوره ای متشکل از دنباله ای از پالس های رادیویی (پالس هایی با پر شدن با فرکانس بالا) وجود نخواهد داشت ، که در آن دوره تکرار ثابت است ، اما مرحله اولیه پر شدن با فرکانس بالا از پالس به پالس تغییر می کند به برخی از قوانین چنین سیگنالهایی تقریباً دوره ای نامیده می شوند. همانطور که بعداً خواهیم دید ، آنها همچنین دارای طیف گسسته ای هستند. ما ماهیت فیزیکی طیف چنین سیگنالهایی را همانند سیگنالهای دوره ای مطالعه خواهیم کرد.

فرم های نگارش سری فوریه سیگنال نامیده می شود تناوبی،اگر شکل آن به صورت چرخه ای در زمان تکرار شود سیگنال دوره ای تو (تی)به طور کلی ، به شرح زیر نوشته شده است:

u (t) = u (t + mT) ، m = 0 ، ± 1 ، ± 2 ،…

در اینجا دوره T سیگنال است. سیگنال های دوره ای می توانند ساده یا پیچیده باشند.

برای نمایش ریاضی سیگنال های دوره ای با یک نقطه تیسری (2.2) اغلب استفاده می شود ، که در آن نوسانات هارمونیک (سینوسی و کسینوس) فرکانس های متعدد به عنوان توابع پایه انتخاب می شوند

y 0 (t) = 1 ؛ y 1 (t) = sinw 1 t ؛ y 2 (t) = cosw 1 t ؛

y 3 (t) = sin2w 1 t ؛ y 4 (t) = cos2w 1 t ؛ ... ، (2.3)

جایی که w 1 = 2p / T فرکانس زاویه ای اساسی دنباله است

کارکرد. برای توابع پایه هارمونیک ، از سری (2.2) سری فوریه را بدست می آوریم (ژان فوریه ریاضیدان و فیزیکدان فرانسوی قرن 19 است).

توابع هارمونیک فرم (2.3) در سری فوریه دارای مزایای زیر هستند: 1) توصیف ریاضی ساده ؛ 2) تغییر ناپذیری در تحولات خطی ، یعنی اگر یک نوسان هارمونیک در ورودی یک مدار خطی عمل کند ، در خروجی آن نیز یک نوسان هارمونیک وجود خواهد داشت ، که فقط در دامنه و فاز اولیه با ورودی متفاوت است. 3) مانند یک سیگنال ، توابع هارمونیک دوره ای هستند و مدت زمان نامحدودی دارند. 4) تکنیک ایجاد توابع هارمونیک بسیار ساده است.

از درس ریاضیات مشخص است که برای گسترش یک سیگنال دوره ای در یک سری در توابع هارمونیک (2.3) ، لازم است شرایط دیریکله را برآورده کنید. اما همه سیگنال های دوره ای واقعی این شرایط را برآورده می کنند و می توانند به عنوان یک سری فوریه ارائه شوند ، که می تواند به یکی از اشکال زیر نوشته شود:

u (t) = A 0/2 + (A ’mn cosnw 1 t + A” mn nw 1 t) ، (2.4)

جایی که ضرایب

یک mn ”= (2.5)

u (t) = A 0/2 + (2.6)

A mn = (2.7)

یا به شکل پیچیده

u (t) = (2.8)

C n = (2.9)

از (2.4) - (2.9) بر می آید که در حالت کلی ، سیگنال دوره ای u (t) شامل یک جزء ثابت A 0/2 و مجموعه ای از نوسانات هارمونیک فرکانس اساسی w 1 = 2pf 1 و هارمونیک های آن است با فرکانس wn = nw 1 ، n = 2 ، 3،4 ، ... هر یک از هارمونیک ها

نوسانات سری فوریه با دامنه و فاز اولیه y n .nn مشخص می شود

نمودار طیفی و طیف یک سیگنال دوره ای. اگر هر سیگنالی به عنوان مجموع نوسانات هارمونیک با فرکانس های مختلف ارائه شود ، گفته می شود که تجزیه طیفیعلامت.

نمودار طیفیسیگنال معمولاً نمای گرافیکی ضرایب سری فوریه این سیگنال نامیده می شود. بین نمودارهای دامنه و فاز تمایز قائل شوید. در شکل 2.6 در مقیاس معین در امتداد محور افقی ، مقادیر فرکانس های هارمونیک ، در امتداد محور عمودی - دامنه آنها A mn و مراحل y n ترسیم می شود. علاوه بر این ، دامنه هارمونیک ها فقط می توانند مقادیر مثبت را دریافت کنند ، مراحل - هم مقادیر مثبت و هم منفی در بازه -p £ y n £ p

طیف سیگنال- مجموعه ای از اجزای هارمونیک با مقادیر خاص فرکانس ، دامنه و مراحل اولیه است که در کل یک سیگنال را تشکیل می دهد. در کاربردهای فنی ، در عمل ، نمودارهای طیفی به طور خلاصه تر نامیده می شوند - طیف دامنه ، طیف فازاغلب آنها به نمودار طیفی دامنه علاقه مند هستند. می توان از آن برای تخمین درصد هارمونیک ها در طیف استفاده کرد.

مثال 2.3 دنباله ای دوره ای از پالس های ویدئویی مستطیلی را در یک سری فوریه گسترش دهید باپارامترهای شناخته شده (U m ، T ، t z) ،حتی "نسبت به نقطه t = 0. یک نمودار طیفی از دامنه ها و فازها در U m = 2B ، T = 20ms ، S = T / t و = 2 و 8 بسازید.

یک سیگنال دوره ای معین در فاصله یک دوره را می توان به صورت نوشت

برای نمایش این سیگنال ، اجازه دهید از فرم نوشتن سری فوریه استفاده کنیم vفرم (2.4). از آنجا که سیگنال یکنواخت است ، فقط اجزای کسینوس در انبساط باقی می مانند.

برنج. 2.6 نمودارهای طیفی یک سیگنال دوره ای:

a - دامنه ؛ ب- فاز

انتگرال یک تابع فرد در یک دوره برابر با صفر است. با استفاده از فرمول (2.5) ، ضرایب را پیدا می کنیم

اجازه نوشتن سری فوریه:

برای ساخت نمودارهای طیفی برای داده های عددی خاص ، i = 0 ، 1 ، 2 ، 3 ، ... را تعیین کرده و ضرایب هارمونیک را محاسبه می کنیم. نتایج محاسبه هشت جزء اول طیف در جدول خلاصه شده است. 2.1 در سری (2.4) A "mn = 0و طبق (2.7) A mn = | A 'mn | ، فرکانس اساسی f 1 = 1 / T = 1 / 20-10 -3 = 50 هرتز ، w 1 = 2pf 1 = 2p * 50 = 314 rad / s به طیف دامنه در شکل.

2.7 برای چنین ساخته شده است n ،که در آن یک منبیش از 5 درصد از حداکثر مقدار

از مثال ارائه شده 2.3 نتیجه می شود که با افزایش چرخه کار ، تعداد اجزای طیفی افزایش می یابد و دامنه آنها کاهش می یابد. گفته می شود چنین سیگنالی دارای طیف غنی است. لازم به ذکر است که برای بسیاری از سیگنالهای عملاً مورد استفاده نیازی به محاسبه دامنه و فازهای هارمونیک ها با توجه به فرمول های قبلی نیست.

جدول 2.1. دامنه اجزای سری فوریه از یک دنباله دوره ای از پالس های مستطیلی

برنج. 2.7 نمودارهای طیفی از یک دنباله دوره ای از پالس ها: آ-با چرخه وظیفه S-2 ؛ - b-when cycle cycle S = 8

در کتابهای مرجع ریاضی جداول تجزیه سیگنال در سری فوریه وجود دارد. یکی از این جداول در پیوست (جدول A.2) آورده شده است.

اغلب این س arال پیش می آید: چند جزء طیفی (هارمونیک) باید برای نشان دادن یک سیگنال واقعی به عنوان یک سری فوریه در نظر گرفته شوند؟ به هر حال ، این سریال ، به طور دقیق ، بی پایان است. در اینجا نمی توان پاسخی بدون ابهام داد. همه چیز بستگی به شکل سیگنال و دقت نمایش آن توسط سری فوریه دارد. تغییر سیگنال روانتر - هارمونیک کمتر مورد نیاز است. اگر سیگنال دارای جهش (ناپیوستگی) باشد ، باید هارمونیک های بیشتری را جمع آوری کرد تا به همان خطا برسیم. با این حال ، در بسیاری از موارد ، به عنوان مثال در تلگراف ، اعتقاد بر این است که سه هارمونیک نیز برای انتقال پالس های مستطیلی با لبه های شیب دار کافی است.

دوره های تجزیه و تحلیل ریاضی

موضوع: محاسبه مجموع جزئی و ویژگیهای طیفی سری فوریه برای یک تابع صریح

عملکرد طیف سیگنال فوریر

1. مدل فرایند فیزیکی

حل مسئله با محاسبات نظری

نمونه ای از حل مسئله

نمونه ای از حل مسئله در محیط Matlab R2009a

کتابشناسی - فهرست کتب

1. مدل فرایند فیزیکی

مدل ریاضی یک سیگنال رادیویی می تواند عملکردی از زمان باشد f(t) . این عملکرد می تواند واقعی یا پیچیده ، تک بعدی یا چند بعدی ، قطعی یا تصادفی (سیگنال های پر سر و صدا) باشد. در مهندسی رادیو هم همینطور مدل ریاضیبا موفقیت برابر جریان ، ولتاژ ، کشش را توصیف می کند میدان الکتریکیو غیره.

سیگنالهای قطعی واقعی تک بعدی را در نظر بگیرید

مجموعه توابع (سیگنال ها) معمولاً به عنوان فضاهای نرمال خطی در نظر گرفته می شوند که در آنها مفاهیم و بدیهیات زیر معرفی می شوند:

) تمام بدیهیات فضای خطی برآورده می شود ؛

) نقطه نقطه دو سیگنال واقعی به شرح زیر تعریف می شود:

اگر دو نقطه سیگنال صفر باشند ، دو سیگنال نامیده می شود.

) سیستم سیگنال های متعامد یک اساس مختصات بی نهایت ابعادی را تشکیل می دهد ، که بر اساس آن هر سیگنال دوره ای متعلق به فضای خطی می تواند تجزیه شود.

در بین سیستم های مختلف توابع متعامد که می توان برای تجزیه سیگنال استفاده کرد ، رایج ترین آنها سیستم توابع هارمونیک (سینوسی و کسینوس) است:

نمایش سیگنال دوره ای معین به عنوان مجموع نوسانات هارمونیک با فرکانس های مختلف ، نمایش طیفی سیگنال نامیده می شود. اجزای هارمونیک فردی سیگنال طیف آن را تشکیل می دهد. از نقطه نظر ریاضی ، بازنمایی طیفی معادل گسترش یک تابع (سیگنال) دوره ای در یک سری فوریه است.

اهمیت تجزیه طیفی توابع در مهندسی رادیو به دلایل متعددی است:

) سادگی مطالعه خواص سیگنال ، زیرا عملکردهای هارمونیک به خوبی درک شده است.

) توانایی تولید یک سیگنال دلخواه ، زیرا تکنیک تولید سیگنال های هارمونیک بسیار ساده است.

) سهولت انتقال و دریافت سیگنال از طریق کانال رادیویی ، tk. نوسان هارمونیک تنها عملکرد زمان است که هنگام عبور از هر مدار خطی شکل خود را حفظ می کند. سیگنال در خروجی مدار با همان فرکانس هارمونیک باقی می ماند ، فقط دامنه و مرحله اولیه نوسان تغییر می کند.

) تجزیه سیگنال به سینوس و کسینوس اجازه می دهد تا از روشی نمادین برای تجزیه و تحلیل انتقال نوسانات هارمونیک از طریق مدارهای خطی استفاده شود.

به عنوان یک مدل از روند فیزیکی ، الکتروکاردیوگرام قلب را در نظر بگیرید.

2. حل مسئله با محاسبات نظری

هدف 1:

اجازه دهید با کمک سری فوریه ، یک ضربه دوره ای تکراری را در ناحیه الکتروکاردیوگرام ، به اصطلاح کمپلکس QRS ، توصیف کنیم.

مجموعه QRS را می توان با تابع خطی قطعه ای زیر تعریف کرد

جایی که

این تابعمی تواند به صورت دوره ای با یک دوره ادامه یابد T = 2l.

سری توابع فوریه:

تعریف 1: تابع فراخوانی می شود بصورت قطعه ای پیوستهدر بخش [a ، b] ، اگر در تمام نقاط این بخش پیوسته باشد ، به جز تعداد محدودی از نقاط که محدودیتهای یک طرفه محدود آن در آن وجود دارد.

تعریف 2:تابع نامیده می شود تکه تکه صافدر برخی از بخشها اگر آن و مشتق آن به صورت قطعه پیوسته باشند.

قضیه 1 (آزمون دیریکله): سری فوریه از یک تابع قطعه-صاف در فاصله f (ایکس) در هر نقطه از تداوم به مقدار تابع در این نقطه و به مقدار در هر نقطه ناپیوستگی همگرا می شود.

عملکرد ما شرایط قضیه را برآورده می کند.

برای یک تابع معین ، ضرایب زیر از سری فوریه را بدست می آوریم:

فرم پیچیده از سری فوریه

برای نمایش مجموعه در فرم پیچیده ، از فرمول های اولر استفاده می کنیم:

اجازه دهید نماد را معرفی کنیم:

سپس می توان سریال را به صورت بازنویسی کرد

علاوه بر این ، ضرایب سری پیچیده فوریه را می توان مستقیماً با محاسبه آنها با فرمول بدست آورد

ما سری فوریه یک تابع معین را به صورت پیچیده می نویسیم

ویژگی های طیفی سریال

اصطلاح در سری فوریه نامیده می شود nهارمونیکمشخص است که

کجا یا

,

بر اساس آن به مصالح گفته می شود دامنه و طیف فازعملکرد دوره ای

طیف ها به صورت گرافیکی به عنوان قطعات طولی کشیده شده اند که عمود بر محوری که مقدار بر روی آن رسم شده است کشیده شده اند n= 1،2 ... یا.

تصویر گرافیکیطیف مربوطه نمودار دامنه یا فاز نامیده می شود. در عمل ، طیف دامنه اغلب استفاده می شود.

.نمونه ای برای حل مشکل

وظیفه 2: در نظر گرفتن مثال خاصوظایف مربوط به مدل انتخابی فرایند فیزیکی.

ما این تابع را به کل محور عددی بسط می دهیم ، تابع دوره ای را بدست می آوریم f(ایکس) با دوره T = 2 ل= 18 (شکل 1.).

برنج. 1. نمودار عملکردی که به صورت دوره ای ادامه دارد

بیایید ضرایب فوریه تابع داده شده را محاسبه کنیم.

بیایید مبالغ جزئی این مجموعه را بنویسیم:

برنج. 2. نمودارهای مبالغ جزئی از سری فوریه

با رشد nنمودارهای مجموع جزئی در نقاط تداوم به نمودار تابع نزدیک می شود f(ایکس) ... در نقاط شکست ، مقادیر مبالغ جزئی نزدیک می شود .

بیایید نمودارهای دامنه و فاز را بسازیم.

یک چهارم داده شد

جدول

4. نمونه ای از حل مسئله در محیط Matlab R2009a

هدف 3:به عنوان مثال ، کل فواصل PR و QT را در نظر بگیرید.

برنج

برای این تابع ، نمودارهایی از مبالغ جزئی ، و همچنین نمودارهای دامنه و فاز بسازید.

بیایید مقادیر خاصی از پارامترها را برای کار خود در نظر بگیریم:

اسکریپتی برای ساخت نمودارها و نمودارهای مورد نیاز.

اسکریپت به شما امکان می دهد با انتخاب پارامترها و مختصات نقاط Q ، R ، S تعدادی از مشکلات مشابه را حل کنید.

٪ محاسبه SUMS های جزئی و ویژگی های اختصاصی سری چهارم برای بیان

٪ تجزیه و تحلیل طیفی. L I1 I2 Q R S I3 I4 I5 P T w v a b cd qr Qy Ry Sy nCase = 18 ؛ = 6 ؛ I2 = 10 ؛ Q = 11 ؛ Qy = -2 ؛ R = 12 ؛ Ry = 17 ؛ S = 13 ؛ Sy = -4 ؛ I3 = 15 ؛ I4 = 20 ؛ I5 = 26 ؛ = 2 ؛ T = 3 ؛ ExprNum = 9 ؛ = 250 ؛ = 30 ؛ = 0 ؛ پرچم == 0 = 1 ؛ (ک<15)

k = منو ("تغییر پارامترها" ، ...

sprintf ("Parameter1 P =٪ g"، P) ، ... ("Parameter2 I1 =٪ g"، I1) ، ... ("Parameter3 I2 =٪ g"، I2) ، ... ("Parameter4 Qx =٪ g "، Q) ، ... (" Parameter5 Qy =٪ g "، Qy) ، ... (" Parameter6 Rx =٪ g "، R) ، ... (" Parameter7 Ry =٪ g "، Ry) ، ... ("Parameter8 Sx =٪ g" ، S) ، ... ("Parameter9 Sy =٪ g" ، Sy) ، ... ("Parameter10 I3 =٪ g" ، I3) ، .. . ("Parameter11 I4 =٪ g" ، I4) ، ... ("Parameter12 T =٪ g"، T) ، ... ("Parameter13 I5 =٪ g"، I5) ، ... ("Parameter13 Ns =٪ g "، Ns) ، ...

"ادامه") ؛ k == 1 ، = ورودی () ؛

endk == 2 ، = ورودی ()؛

endk == 3 ، = ورودی ()؛

endk == 4 ، = ورودی ()؛

endk == 5 ، = ورودی ()؛

endk == 6 ، = ورودی ()؛

endk == 7 ، = ورودی () ؛

"مقدار Sx جدید ="])؛

endk == 9 ، = ورودی ()؛

endk == 10 ، = ورودی () ؛

endk == 11 ، = ورودی ()؛

endk == 12 ، = ورودی ()؛

endk == 13 ، = ورودی ()

endk == 14 ، = ورودی ()

Application کاربرد پارامترها = Qy / (Q-I2) ؛

v = Qy * I2 / (I2-Q) ؛ = (Ry-Qy) / (RQ) ؛ = (Qy * RQ * Ry) / (RQ) ؛ = (Sy-Ry) / (SR) ؛ = (Ry * SR * Sy) / (SR) ؛ = Sy / (S-I3) ؛ = I3 * Sy / (I3-S) ؛ = 2 * L / N ؛ = 0: Ts: 2 * L ؛ = طول (t ) ؛ = صفر (1 ، Dim) ؛ = طبقه (I1 * N / 2 / L) +1 ؛ = طبقه ((I2-I1) * N / 2 / L) +1 ؛ = طبقه ((Q-I2) * N / 2 / L) +1 ؛ = طبقه ((RQ) * N / 2 / L) +1 ؛ = طبقه ((SR) * N / 2 / L) +1 ؛ = طبقه ((I3-S) * N / 2 / L) +1 ؛ = طبقه ((I4-I3) * N / 2 / L) +1 ؛ = طبقه ((I5-I4) * N / 2 / L) +1 ؛ = طبقه (( 2 * L-I4) * N / 2 / L) +1 ؛ i = 1: u1 (i) = P * sin (pi * t (i) / I1) ؛ i = u1: u2 (i) = 0 ؛ i = (u2 + u1) :( u3 + u2 + u1) (i) = w * t (i) + v؛ i = (u3 + u2 + u1): (u4 + u3 + u2 + u1) (i) = a * t (i) + b ؛ i = (u4 + u3 + u2 + u1): (u5 + u4 + u3 + u2 + u1) (i) = c * t (i) + d ؛ i = (u5 + u4 + u3 + u2 + u1): (u6 + u5 + u4 + u3 + u2 + u1) (i) = q * t (i) + r؛ i = (u6 + u5 + u4 + u3 + u2 + u1 ): (u7 + u6 + u5 + u4 + u3 + u2 + u1) (i) = 0 ؛ i = (u7 + u6 + u5 + u4 + u3 + u2 + u1): (u8 + u7 + u6 + u5 + u4 + u3 + u2 + u1) (i) = T * sin (pi * (t (i) -I4) / (I5 -I4)) ؛ (t ، y ، "عرض خط" ، 2) ، شبکه ، مجموعه ( gca ، "FontName" ، "Arial Cyr" ، "FontSize" ، 16)؛

عنوان ("نمودار روند") ؛ xlabel ("زمان (ها)") ؛ ylabel ("Y (t)") ؛

plot مجموع جزئی ناحیه n

n = 0؛ j = 1: ExprNum = j؛ j1 = quad (f، 0، I1)؛ 2 = a0 + quad (f، I1، I2)؛ 3 = a0 + quad (f، I2، Q )؛ 4 = a0 + quad (f، Q، R)؛ 5 = a0 + quad (f، R، S)؛ 6 = a0 + quad (f، S، I3)؛ 7 = a0 + quad ( f، I3، I4)؛ 8 = a0 + quad (f، I4، I5)؛ 9 = a0 + quad (f، I5، 2* L)؛ = a0 / L؛ = صفر (1، Ns) ؛ = صفر (1 ، Ns) ؛ i = 1: Ns = i ؛ j = 1: ExprNum = j ؛ j1 (i) = quad (f، 0، I1) ؛ (i) = quad (g ، 0 ، I1) ؛ 2 (i) = an (i) + quad (f، I1، I2) ؛ (i) = bn (i) + quad (g، I1، I2) ؛ 3 (i) = an (i) + quad (f، I2، Q)؛ (i) = bn (i) + quad (g، I2، Q)؛ 4 (i) = an (i) + quad (f، Q ، R) ؛ (i) = bn (i) + quad (g ، Q، R) ؛ 5 (i) = an (i) + quad (f، R، S) ؛ (i) = bn (i ) + quad (g، R، S)؛ 6 (i) = an (i) + quad (f، S، I3)؛ (i) = bn (i) + quad (g، S، I3) ؛ 7 (i) = an (i) + quad (f، I3، I4) ؛ (i) = bn (i) + quad (g، I3، I4) ؛ 8 (i) = an (i) + quad (f، I4، I5)؛ (i) = bn (i) + quad (g، I4، I5)؛ 9 (i) = an (i) + quad (f، I5، 2* L) ؛ (i) = bn (i) + quad (g ، I5 ، 2* L) ؛ (i) = an (i) / L ؛ (i) = bn (i) / L ؛ = t ؛ = صفر (1 ، طول (x)) ؛ = fn + a0 / 2 ؛ i = 1: Ns = i ؛ = fn + an (i) * cos (n * pi * x / L) + bn (i) * sin (n * pi * x / L) ؛ (t ، y ، x ، fn ، "LineWidth" ، 2) ، grid ، set (gca ، "FontName" ، "Arial Cyr" ، "FontSize" ، 16) ؛

عنوان ("نمودار سیگنال و مجموع جزئی") ؛ xlabel ("زمان (ها)") ؛ ylabel (sprintf ("Sn (t)")) ؛

٪ رسم نمودار دامنه = صفر (1 ، Ns) ؛

wn = pi / L ؛ = wn: wn: wn * Ns ؛ i = 1: Ns (i) = sqrt (an (i). ^ 2 + bn (i). ^ 2) ؛ (Gn ، A ، ". ") ، grid ، set (gca ،" FontName "،" Arial Cyr "،" FontSize "، 16) ؛ (" نمودار دامنه سیگنال ") ؛ xlabel ("n") ؛ ylabel ("An") ؛

Construction ساخت نمودار فاز سیگنال = صفر (1 ، Ns) ؛

برای i = 1: Ns (an (i)> 0) (i) = atan (bn (i) / an (i)) ؛ ((an (i)<0)&&(bn(i))>0) (i) = آتان (bn (i) / an (i)) + pi ؛ ((an (i)<0)&&(bn(i))<0)(i)=pi-atan(bn(i)/an(i));((an(i)==0)&&(bn(i))>0) (i) = pi / 2؛ ((an (i) == 0) && (bn (i))<0)(i)=-pi/2;(Gn,Fi,"."), grid, set(gca,"FontName","Arial Cyr","FontSize",16);("Фазовая диаграмма сигнала"); xlabel("n"); ylabel("Fi");Figure 1;Figure 2;Figure 3;Figure 4;=0;=input("Закончить работу-<3>، ادامه دهید - ");

لیستادبیات

1. Fikhtengolts ، G.M. دوره حساب دیفرانسیل و انتگرال: در 3 جلد ، مسکو ، 1997.3 جلد.

Vodnev، V.T.، Naumovich، A.F.، Naumovich، N.F.، فرمول های اساسی ریاضی. مینسک ، 1998

خارکویچ ، A.A. ، طیف و تجزیه و تحلیل. مسکو ، 1958

لازارف ، یو. اف. ، آغاز برنامه نویسی در محیط MatLAB. کیف 2003

دمیدوویچ ، B.P. مجموعه مسائل و تمرینات در تحلیل ریاضی ، م. ، 1988.

در میان سیستم های مختلف توابع متعامد که می توانند به عنوان پایه ای برای ارائه سیگنال های مهندسی رادیو استفاده شوند ، یک مکان استثنایی توسط توابع هارمونیک (سینوسی و کسینوس) اشغال شده است. اهمیت سیگنال های هارمونیک برای مهندسی رادیو به دلایل مختلفی است.

به خصوص:

1. سیگنالهای هارمونیک نسبت به تغییراتی که توسط مدارهای الکتریکی خطی ثابت انجام می شود ، تغییرناپذیر هستند. اگر چنین مداری توسط منبع نوسانات هارمونیک برانگیخته شود ، سیگنال خروجی مدار با همان فرکانس هارمونیک باقی می ماند و تنها در دامنه و فاز اولیه از سیگنال ورودی متفاوت است.

2. تکنیک تولید سیگنال های هارمونیک نسبتاً ساده است.

اگر هر سیگنالی به عنوان مجموع نوسانات هارمونیک با فرکانس های مختلف ارائه شود ، گفته می شود تجزیه طیفی این سیگنال انجام شده است. اجزای هارمونیک فردی سیگنال طیف آن را تشکیل می دهد.

2.1 سیگنال های دوره ای و سری فوریه

مدل ریاضی یک فرآیند که در زمان تکرار می شود یک سیگنال دوره ای با ویژگی زیر است:

در اینجا T دوره سیگنال است.

کار این است که تجزیه طیفی چنین سیگنالی را بیابیم.

سری فوریه.

اجازه دهید فاصله زمانی در نظر گرفته شده در فصل را تعیین کنیم. من اساس متعارف توسط توابع هارمونیک با فرکانس های متعدد تشکیل شده است.

هر تابع از این اساس شرط تناوبی را برآورده می کند (2.1). بنابراین ، - با تجزیه عمودی سیگنال بر این اساس ، یعنی محاسبه ضرایب

ما تجزیه طیفی را بدست می آوریم

که در تمام بی نهایت محور زمان معتبر است.

مجموعه ای از فرم (2.4) را سری فوریه سیگنال داده شده می نامند. اجازه دهید فرکانس اساسی دنباله ای را که سیگنال دوره ای را تشکیل می دهد ، معرفی کنیم. با محاسبه ضرایب انبساط با فرمول (2.3) ، سری فوریه را برای یک سیگنال دوره ای می نویسیم

با ضرایب

(2.6)

بنابراین ، در حالت کلی ، یک سیگنال دوره ای شامل یک جزء ثابت مستقل از زمان و مجموعه ای بی نهایت از نوسانات هارمونیک است ، که به اصطلاح هارمونیک با فرکانس هایی است که چند برابر فرکانس اساسی دنباله هستند.

هر هارمونیک را می توان با دامنه و فاز اولیه آن توصیف کرد. بدین منظور ، ضرایب سری فوریه باید به شکل نوشته شوند

با جایگزینی این عبارات در (2.5) ، ما یک فرم دیگر ، - معادل سری فوریه را بدست می آوریم:

که گاهی راحت تر است

نمودار طیفی یک سیگنال دوره ای

بنابراین مرسوم است که یک نمای گرافیکی از ضرایب سری فوریه را برای یک سیگنال خاص فراخوانی کنیم. تفاوت بین نمودارهای طیفی دامنه و فاز (شکل 2.1).

در اینجا ، در محور افقی ، در مقیاس مشخص ، فرکانس های هارمونیک ها رسم می شود و در محور عمودی ، دامنه ها و مراحل اولیه آنها ترسیم می شود.

برنج. 2.1 نمودارهای طیفی برخی از سیگنال های دوره ای: a - دامنه ؛ ب - فاز

آنها به خصوص به نمودار دامنه علاقه مند هستند ، که این امر امکان قضاوت در مورد درصد هارمونیکهای خاص در طیف یک سیگنال دوره ای را ممکن می سازد.

بیایید چند نمونه خاص را بررسی کنیم.

مثال 2.1 سری فوریه از یک دنباله دوره ای از پالس های ویدئویی مستطیلی با پارامترهای شناخته شده ، حتی نسبت به نقطه t = 0.

در مهندسی رادیو ، این نسبت را چرخه وظیفه دنباله می نامند. با استفاده از فرمول ها (2.6) ، می یابیم

راحت است فرمول نهایی سری فوریه را در فرم بنویسید

در شکل 2.2 نمودارهای دامنه دنباله مورد نظر را در دو مورد شدید نشان می دهد.

توجه به این نکته ضروری است که دنباله ای از پالس های کوتاه ، که به ندرت یکدیگر را دنبال می کنند ، دارای ترکیب طیفی غنی هستند.

برنج. 2.2 طیف دامنه یک دنباله دوره ای از پالس های ویدئویی مستطیلی: الف - در چرخه وظیفه بالا ؛ ب - در چرخه کم کار

مثال 2.2. سری فوریه از یک پالس دوره ای با یک سیگنال هارمونیک فرم محدود در سطح (فرض می شود) تشکیل شده است.

ما یک پارامتر خاص را معرفی می کنیم - زاویه قطع ، که از رابطه از کجا تعیین می شود

مطابق با این ، مقدار برابر با طول یک پالس است که در اندازه زاویه ای بیان شده است:

پرونده تحلیلی نبض تولید کننده دنباله مورد بررسی دارای فرم است

جزء ثابت دنباله

ضریب دامنه هارمونیک اول

به طور مشابه ، دامنه محاسبه می شود - اجزای هارمونیک در

نتایج بدست آمده معمولاً به شرح زیر نوشته می شود:

جایی که به اصطلاح برگ عمل می کند:

نمودارهای برخی از توابع برگ در شکل نشان داده شده است. 2.3

برنج. 2.3 نمودارهای چند تابع برگ اول

فرم پیچیده از سری فوریه.

تجزیه طیفی یک سیگنال دوره ای نیز می تواند تا حدودی یونی ، با استفاده از یک سیستم از توابع پایه متشکل از نمایی با نماهای خیالی انجام شود:

به راحتی می توان دریافت که عملکردهای این سیستم دوره ای است و یک دوره در یک فاصله زمانی متعارف از آن زمان عادی شده است

سری فوریه از یک سیگنال دوره ای دلخواه در این مورد شکل می گیرد

با ضرایب

معمولاً از شکل زیر نماد استفاده می شود:

Expression (2.11) یک سری فوریه به شکل پیچیده است.

طیف سیگنال مطابق با فرمول (2.11) شامل اجزایی در نیم محور فرکانس منفی است و. به عنوان مثال ، در سری (2.11) ، اصطلاحات با فرکانس های مثبت و منفی به صورت جفت ترکیب می شوند.

در بسیاری از موارد ، کار به دست آوردن (محاسبه) طیف سیگنال به شرح زیر است. یک ADC وجود دارد که با نرخ نمونه برداری Fd یک سیگنال پیوسته را که در طول زمان T به ورودی آن می رسد به نمونه های دیجیتالی - قطعات N تبدیل می کند. در مرحله بعد ، آرایه نمونه ها وارد برنامه ای می شود که N / 2 برخی از مقادیر عددی را خروجی می دهد (برنامه نویسی که از اینترنت حذف شده استبرنامه ای نوشت ، ادعا می کند که تبدیل فوریه را انجام می دهد).

برای بررسی اینکه آیا برنامه به درستی کار می کند ، بیایید مجموعه ای از نمونه ها را به عنوان مجموع دو sinusoid sin (10 * 2 * pi * x) + 0.5 * sin (5 * 2 * pi * x) تشکیل دهیم و آن را در برنامه قرار دهیم به برنامه موارد زیر را ترسیم کرد:

شکل 1 نمودار عملکرد زمان سیگنال

شکل 2 نمودار طیف سیگنال

در نمودار طیف ، دو چوب (هارمونیک) 5 هرتز با دامنه 0.5 ولت و 10 هرتز وجود دارد - با دامنه 1 ولت ، همه چیز در فرمول سیگنال اصلی است. همه چیز خوب است ، برنامه نویس خوب! برنامه به درستی کار می کند.

این بدان معناست که اگر یک سیگنال واقعی از مخلوط دو سینوسی به ورودی ADC اعمال کنیم ، طیفی مشابه شامل دو هارمونیک به دست می آید.

در کل ، ما واقعیسیگنال اندازه گیری شده ، به مدت 5 ثانیه، ADC دیجیتالی شده ، یعنی ارائه شده است گسستهمی شمارد ، دارد غیر دوره ای مجزاطیف

از نظر ریاضی ، چند اشتباه در این عبارت وجود دارد؟

اکنون مدیران تصمیم گرفتند ما تصمیم گرفتیم که 5 ثانیه خیلی طولانی است ، اجازه دهید سیگنال را در 0.5 ثانیه اندازه گیری کنیم.



شکل 3 نمودار عملکرد sin (10 * 2 * pi * x) + 0.5 * sin (5 * 2 * pi * x) در یک دوره اندازه گیری 0.5 ثانیه

شکل 4 طیف عملکرد

به نظر می رسد چیزی اشتباه است! هارمونیک 10 هرتز به طور معمول کشیده شده است و به جای چوب 5 هرتز ، چند هارمونیک نامفهوم ظاهر شد. ما در اینترنت نگاه می کنیم ، چه و چگونه ...

در ، آنها می گویند که باید صفرها به انتهای نمونه اضافه شود و طیف طبیعی عادی شود.

شکل 5 صفر را تا 5 ثانیه به پایان رساندیم

شکل 6 طیف را دریافت کرد

هنوز آن چیزی که در 5 ثانیه بود ، نبود. ما باید با نظریه برخورد کنیم. قابل اعتماد و متخصص ویکیپدیا- منبع دانش

2. عملکرد پیوسته و نمایش آن توسط سری فوریه

از نظر ریاضی ، سیگنال ما با مدت زمان T ثانیه تابع f (x) است که در فاصله (0 ، T) تعریف شده است (X در این حالت زمان است). چنین عملکردی همیشه می تواند به عنوان مجموعه ای از توابع هارمونیک (سینوسی یا کسینوس) به شکل نشان داده شود:

(1) ، جایی که:

K - تعداد عملکرد مثلثاتی (تعداد جزء هارمونیک ، تعداد هارمونیک)
T - قسمتی که عملکرد در آن تعریف شده است (مدت زمان سیگنال)
Ak دامنه جزء هارمونیک K است ،
θk مرحله اولیه مولفه هارمونیک kth است

"نمایش یک تابع به عنوان مجموع یک سری" به چه معناست؟ این بدان معناست که با افزودن مقادیر اجزای هارمونیک سری فوریه ، مقدار عملکرد خود را در این نقطه بدست می آوریم.

(دقیق تر ، انحراف ریشه میانگین مربع سری از تابع f (x) به صفر می رسد ، اما با وجود همگرایی ریشه میانگین مربع ، سری فوریه تابع ، به طور کلی ، موظف نیست به صورت نقطه ای به آن همگرا شوید. به https://ru.wikipedia.org/ wiki/ Fourier_Row مراجعه کنید.)

این مجموعه را می توان به صورت زیر نیز نوشت:

(2),
جایی که دامنه پیچیده k-th.

رابطه بین ضرایب (1) و (3) با فرمول های زیر بیان می شود:

توجه داشته باشید که هر سه نمایندگی از سری فوریه کاملاً معادل هستند. گاهی اوقات ، هنگام کار با مجموعه فوریه ، راحت تر است که از نمایندگان استدلال خیالی به جای سینوس ها و کسینوس ها استفاده کنیم ، یعنی از تبدیل فوریه به شکل پیچیده استفاده کنیم. اما برای ما راحت است که از فرمول (1) استفاده کنیم ، جایی که سری فوریه به عنوان مجموع امواج کسینوس با دامنه ها و فازهای مربوطه ارائه می شود. در هر صورت ، اشتباه است که گفته شود نتیجه تبدیل فوریه یک سیگنال واقعی دامنه های پیچیده هارمونیک ها خواهد بود. همانطور که ویکی می گوید ، "تبدیل فوریه (ℱ) عملیاتی است که یک تابع را به یک متغیر واقعی به یک تابع دیگر و همچنین یک متغیر واقعی اختصاص می دهد."

جمع:
مبنای ریاضی تجزیه و تحلیل طیفی سیگنالها تبدیل فوریه است.

تبدیل فوریه به شما این امکان را می دهد که تابع پیوسته f (x) (سیگنال) را که بر روی بخش (0 ، T) تعریف شده است به عنوان مجموع تعداد بی نهایت (سری بی نهایت) از توابع مثلثاتی (سینوسی و \ یا امواج کسینوس) با دامنه ها و فازهای خاصی که در بخش (0 ، T) نیز در نظر گرفته شده است. به چنین سریالی سری فوریه می گویند.

بیایید به چند نکته دیگر توجه کنیم که درک آنها برای کاربرد صحیح تبدیل فوریه در تحلیل سیگنال ضروری است. اگر سری فوریه (مجموع سینوسی ها) را در کل محور X در نظر بگیریم ، می بینیم که در خارج از بخش (0 ، T) تابع نشان داده شده توسط سری فوریه به صورت دوره ای عملکرد ما را تکرار می کند.

به عنوان مثال ، در نمودار شکل 7 ، تابع اصلی در بازه (-T \ 2 ، + T \ 2) تعریف شده است ، و سری فوریه نشان دهنده یک تابع دوره ای است که در کل محور x تعریف شده است.

این به این دلیل است که سینوسوئیدها خود عملکردهای دوره ای هستند و بر این اساس ، مجموع آنها یک تابع دوره ای خواهد بود.

شکل 7 نمایش یک عملکرد اصلی غیر دوره ای توسط سری فوریه

بدین ترتیب:

عملکرد اصلی ما پیوسته و غیر دوره ای است که بر روی بخشی از طول T تعریف شده است.
طیف این عملکرد گسسته است ، یعنی در قالب مجموعه ای بی نهایت از اجزای هارمونیک - سری فوریه ارائه شده است.
در واقع ، سری فوریه یک تابع دوره ای خاص را مشخص می کند که با بخش ما منطبق است (0 ، T) ، اما برای ما این دوره ای ضروری نیست.

دوره های اجزای هارمونیک چند برابر مقدار قطعه (0 ، T) است که بر روی آنها تابع اصلی f (x) تعریف شده است. به عبارت دیگر ، دوره های هارمونیک چند برابر مدت زمان اندازه گیری سیگنال است. به عنوان مثال ، دوره اولین هارمونیک از سری فوریه برابر با فاصله T است که بر روی آن تابع f (x) تعریف شده است. دوره هارمونیک دوم از سری فوریه برابر با فاصله T / 2 است. و غیره (شکل 8 را ببینید).

شکل 8 دوره (فرکانس) اجزای هارمونیک سری فوریه (در اینجا T = 2π)

بر این اساس ، فرکانس های اجزای هارمونیک چند برابر 1 / T است. یعنی فرکانسهای اجزای هارمونیک Fk برابر Fk = k \ T است ، جایی که k از 0 تا ranges متغیر است ، برای مثال k = 0 F0 = 0 ؛ k = 1 F1 = 1 \ T ؛ k = 2 F2 = 2 \ T ؛ k = 3 F3 = 3 \ T ؛… Fk = k \ T (در فرکانس صفر - جزء ثابت).

اجازه دهید عملکرد اصلی ما یک سیگنال ثبت شده در طول T = 1 ثانیه باشد. سپس دوره اولین هارمونیک برابر با مدت زمان سیگنال ما T1 = T = 1 ثانیه و فرکانس هارمونیک 1 هرتز خواهد بود. دوره هارمونیک دوم برابر با مدت زمان سیگنال تقسیم بر 2 (T2 = T / 2 = 0.5 ثانیه) و فرکانس 2 هرتز خواهد بود. برای هارمونیک سوم ، T3 = T / 3 ثانیه و فرکانس آن 3 هرتز است. و غیره.

مرحله بین هارمونیک ها در این مورد 1 هرتز است.

بنابراین ، یک سیگنال با مدت زمان 1 ثانیه می تواند به اجزای هارمونیک (برای به دست آوردن طیف) با وضوح فرکانس 1 هرتز تجزیه شود.
برای افزایش وضوح 2 برابر تا 0.5 هرتز ، لازم است مدت زمان اندازه گیری را 2 برابر - تا 2 ثانیه افزایش دهید. یک سیگنال با مدت زمان 10 ثانیه می تواند به اجزای هارمونیک (برای به دست آوردن طیف) با وضوح فرکانس 0.1 هرتز تجزیه شود. هیچ راه دیگری برای افزایش وضوح فرکانس وجود ندارد.

راهی برای افزایش مصنوعی مدت زمان سیگنال با افزودن صفر به آرایه نمونه وجود دارد. اما وضوح فرکانس واقعی را افزایش نمی دهد.

3. سیگنال های گسسته و تبدیل فوریه گسسته

با توسعه فناوری دیجیتال ، روش های ذخیره داده های اندازه گیری (سیگنال) نیز تغییر کرده است. اگر قبلاً می توان سیگنال را روی ضبط صوت ضبط کرد و به صورت آنالوگ روی نوار ذخیره کرد ، اکنون سیگنالها دیجیتالی شده و در قالب مجموعه اعداد (شمارش) در پرونده ها در حافظه کامپیوتر ذخیره می شوند.

یک طرح معمولی برای اندازه گیری و دیجیتالی شدن سیگنال به شرح زیر است.

شکل 9 نمودار نمودار اندازه گیری

سیگنال مبدل اندازه گیری برای مدتی به ADC می رسد T. نمونه های سیگنال (نمونه) که در طول زمان T به دست آمده به کامپیوتر منتقل شده و در حافظه ذخیره می شود.

شکل 10 سیگنال دیجیتالی - N نمونه ای که در طول زمان T به دست آمده است

الزامات پارامترهای دیجیتالی شدن سیگنال چیست؟ دستگاهی که یک سیگنال آنالوگ ورودی را به یک کد گسسته (سیگنال دیجیتال) تبدیل می کند ، مبدل آنالوگ به دیجیتال (ADC) (ویکی) نامیده می شود.

یکی از پارامترهای اصلی ADC حداکثر میزان نمونه برداری (یا نرخ نمونه برداری ، نرخ نمونه انگلیسی) است - میزان نمونه برداری از یک سیگنال پیوسته در زمان در طول نمونه گیری آن. اندازه گیری در هرتز ((ویکی))

با توجه به قضیه کوتلنیکوف ، اگر یک سیگنال پیوسته دارای طیفی با فرکانس Fmax باشد ، می توان آن را به طور کامل و بدون ابهام از نمونه های گسسته خود که در فواصل زمانی گرفته شده بازسازی کرد. ، یعنی با فرکانس Fd ≥ 2 * Fmax ، که Fd فرکانس نمونه گیری است ؛ Fmax حداکثر فرکانس طیف سیگنال است. به عبارت دیگر ، فرکانس نمونه برداری سیگنال (فرکانس نمونه برداری ADC) باید حداقل 2 برابر بیشتر از حداکثر فرکانس سیگنالی باشد که می خواهیم اندازه گیری کنیم.

و اگر نمونه هایی با فرکانس کمتر از حد مورد نیاز قضیه کوتلنیکوف بگیریم ، چه اتفاقی می افتد؟

در این مورد ، اثر "aliasing" (معروف به اثر استروبوسکوپی ، اثر moiré) رخ می دهد ، که در آن یک سیگنال با فرکانس بالا ، پس از دیجیتالی شدن ، به یک سیگنال با فرکانس پایین تبدیل می شود ، که در واقع وجود ندارد. در شکل 11 موج سینوسی قرمز با فرکانس بالا یک سیگنال واقعی است. یک سینوسی آبی با فرکانس پایین یک سیگنال ساختگی است که به دلیل این واقعیت ایجاد می شود که در طول زمان نمونه برداری بیش از نیمی از دوره سیگنال با فرکانس بالا را عبور می دهد.

برنج. 11. ظاهر شدن یک سیگنال کاذب با فرکانس پایین با نرخ نمونه برداری به اندازه کافی بالا

برای جلوگیری از تأثیر aliasing ، یک فیلتر ضد aliasing مخصوص در مقابل ADC نصب شده است-یک فیلتر کم گذر (فیلتر کم گذر) ، که فرکانس های زیر نیمی از فرکانس نمونه برداری ADC را عبور می دهد و فرکانس های بالاتر را قطع می کند.

برای محاسبه طیف سیگنال از نمونه های گسسته آن ، از تبدیل گسسته فوریه (DFT) استفاده می شود. دوباره توجه داشته باشید که طیف سیگنال گسسته "با تعریف" با فرکانس Fmax ، کمتر از نیمی از فرکانس نمونه برداری Fd ، محدود شده است. بنابراین ، طیف یک سیگنال گسسته را می توان با مجموع تعداد محدود هارمونیک ها نشان داد ، بر خلاف مجموع بی نهایت برای سری فوریه یک سیگنال پیوسته ، که طیف آن می تواند نامحدود باشد. طبق قضیه کوتلنیکوف ، حداکثر فرکانس یک هارمونیک باید به گونه ای باشد که حداقل دو عدد داشته باشد ، بنابراین تعداد هارمونیک ها برابر با نصف تعداد نمونه های یک سیگنال گسسته است. یعنی اگر N نمونه در نمونه وجود داشته باشد ، تعداد هارمونیک ها در طیف برابر با N / 2 خواهد بود.

اکنون تبدیل گسسته فوریه (DFT) را در نظر بگیرید.

مقایسه با سری فوریه

ما می بینیم که آنها همزمان هستند ، با این تفاوت که زمان در DFT گسسته است و تعداد هارمونیک ها به N / 2 محدود می شود ، که نصف تعداد شمارش است.

فرمولهای DFT با متغیرهای صحیح بدون بعد k ، s نوشته می شوند ، جایی که k تعداد نمونه های سیگنال ، s تعداد اجزای طیفی است.
مقدار s تعداد نوسانات کل هارمونیک را در دوره T (مدت زمان اندازه گیری سیگنال) نشان می دهد. از تبدیل فوریه گسسته برای یافتن دامنه و فازهای هارمونیک ها به صورت عددی استفاده می شود ، به عنوان مثال. "روی کامپیوتر"

بازگشت به نتایج در ابتدا. همانطور که در بالا ذکر شد ، هنگام گسترش یک تابع غیر دوره ای (سیگنال ما) در یک سری فوریه ، سری فوریه حاصل در واقع مربوط به یک تابع دوره ای با یک دوره T است (شکل 12).

شکل 12 تابع دوره ای f (x) با دوره T0 ، با دوره اندازه گیری T> T0

همانطور که در شکل 12 مشاهده می شود ، تابع f (x) دوره ای با دوره T0 است. با این حال ، با توجه به این که مدت نمونه اندازه گیری T با دوره تابع T0 منطبق نیست ، تابع بدست آمده به عنوان سری فوریه دارای یک ناپیوستگی در نقطه T است. در نتیجه ، طیف این تابع شامل تعداد زیادی هارمونیک با فرکانس بالا است. اگر مدت زمان نمونه اندازه گیری T با دوره تابع T0 همزمان باشد ، در طیف بدست آمده پس از تبدیل فوریه ، فقط اولین هارمونیک وجود خواهد داشت (سینوسی با دوره برابر با مدت نمونه) ، زیرا تابع f (x) یک سینوسی است.

به عبارت دیگر ، برنامه DFT "نمی داند" که سیگنال ما یک "قطعه سینوسی" است ، اما سعی می کند یک عملکرد دوره ای را به عنوان یک سری نشان دهد ، که به دلیل ناسازگاری قطعات منفرد سینوسی دارای ناپیوستگی است.

در نتیجه ، هارمونیک ها در طیف ظاهر می شوند ، که باید شکل عملکرد ، از جمله این ناپیوستگی را خلاصه کنند.

بنابراین ، برای به دست آوردن طیف "صحیح" یک سیگنال ، که مجموع چندین سینوسی با دوره های مختلف است ، لازم است که تعداد صحیح دوره های هر سینوسی در دوره اندازه گیری سیگنال قرار گیرد. در عمل ، این شرط را می توان برای مدت زمان اندازه گیری سیگنال به اندازه کافی طولانی برآورده کرد.

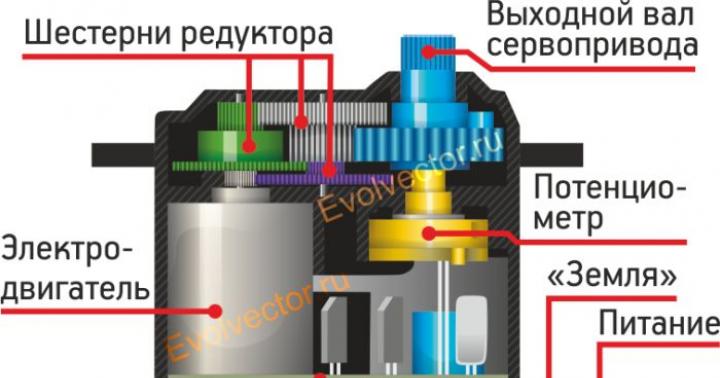
شکل 13 مثال از عملکرد و طیف سیگنال خطای سینماتیکی گیربکس

با مدت زمان کوتاه تر ، تصویر "بدتر" به نظر می رسد:

شکل 14 مثال از عملکرد و طیف سیگنال ارتعاش روتور

در عمل ، درک اینکه "اجزای واقعی" کجا هستند ، و "مصنوعات" در کجا ناشی از این واقعیت است که دوره های اجزاء و مدت زمان نمونه برداری سیگنال چند برابر نیست ، یا "جهش و شکاف "شکل موج. البته کلمات "اجزای واقعی" و "مصنوعات" بیهوده در نقل قول گرفته نشده اند. وجود بسیاری از هارمونیک ها بر روی نمودار طیف به این معنا نیست که سیگنال ما در واقعیت از آنها "تشکیل شده است". مانند این است که تصور کنیم که شماره 7 "شامل" اعداد 3 و 4 است. عدد 7 را می توان به عنوان مجموع اعداد 3 و 4 نشان داد - این درست است.

بنابراین سیگنال ما ... یا بهتر بگویم حتی "سیگنال ما" نیست ، بلکه یک تابع دوره ای که با تکرار سیگنال (نمونه) ما تشکیل شده است ، می تواند به عنوان مجموع هارمونیک ها (سینوسی ها) با دامنه ها و فازهای مشخص نشان داده شود. اما در بسیاری از مواردی که برای تمرین مهم هستند (شکلهای بالا را ببینید) ، واقعاً می توان هارمونیکهای بدست آمده در طیف را با فرایندهای واقعی که ماهیت چرخه ای دارند و سهم بسزایی در شکل سیگنال دارند مرتبط کرد.

برخی نتایج

1. سیگنال اندازه گیری شده واقعی ، مدت زمان T ثانیه ، دیجیتالی شده توسط ADC ، یعنی نشان داده شده توسط مجموعه ای از نمونه های مجزا (قطعات N) ، دارای طیف غیر دوره ای مجزا است که توسط مجموعه ای از هارمونیک ها (N / 2 قطعه) نشان داده می شود. )

2. سیگنال با مجموعه ای از مقادیر واقعی و طیف آن با مجموعه ای از مقادیر واقعی نشان داده می شود. فرکانس هارمونیک مثبت است. این واقعیت که ریاضیدانان راحت تر می دانند که طیف را به صورت پیچیده با استفاده از فرکانس های منفی نشان دهند ، به این معنا نیست که "این درست است" و "این کار همیشه باید انجام شود".

3. سیگنال اندازه گیری شده در فاصله زمانی T فقط در بازه زمانی T تعیین می شود. آنچه که قبل از شروع اندازه گیری سیگنال اتفاق افتاده بود و بعد از آن چه خواهد شد ، برای علم ناشناخته است. و در مورد ما ، جالب نیست. DFT یک سیگنال محدود به زمان ، طیف "واقعی" خود را ارائه می دهد ، به این معنا که در شرایط خاص ، به فرد اجازه می دهد دامنه و فرکانس اجزای آن را محاسبه کند.

مواد مورد استفاده و سایر مواد مفید.