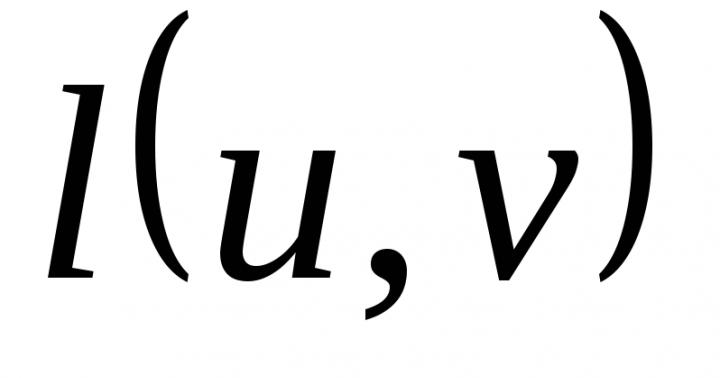NOUS TROUVONS NOMBRE DE FIBONACCI NOUS NOUVEAUX DE TROIS DE MOYENS POUR UN TEMPS ACCEPTABLE: Les bases de la programmation dynamique. Numéros de Fibonacci: Cycle et récursivité FIBONACCI FIBONACCI Fonction

Très souvent sur une variété d'Olympiades, des tâches semblent être comme ceci, ce qui, comme pensée à première vue, peut être résolu avec une simple brise. Mais si nous calculons le nombre d'options possibles, il est immédiatement convaincu de l'inefficacité de cette approche: par exemple, une simple fonction récursive ci-dessous consomme des ressources substantielles sur le 30ème numéro de Fibonacci, alors que sur les Jeux olympiques, le temps de la solution est souvent limité à 1-5 secondes.

Int fibo (int n) (si (n \u003d\u003d 1 || n \u003d\u003d 2) (retour 1;) Autres (Retour Fibo (N - 1) + Fibo (N-2);))

Pensons à pourquoi cela se produit. Par exemple, pour calculer FIBO (30), nous calculons d'abord FIBO (29) et FIBO (28). Mais en même temps, notre programme "oublie" que FIBO (28) nous déjà calculé Lors de la recherche de FIBO (29).

L'erreur principale de cette approche "dans le front" est que les mêmes valeurs des arguments de la fonction sont calculées à plusieurs reprises - et il s'agit d'opérations suffisantes à forte intensité de ressources. La méthode de programmation dynamique nous aidera à vous débarrasser de l'informatique dynamique - il s'agit d'une réception, lors de l'utilisation de la tâche, la tâche est divisée en sous-tâches générales et répétez des sous-tâches, chacune d'une solution seulement 1 fois - cela améliore considérablement l'efficacité du programme. . Cette méthode est décrite en détail dans, il existe également des exemples de résolution d'autres tâches.

L'option la plus simple d'améliorer notre fonction est de mémoriser les valeurs que nous avons déjà calculées. Pour ce faire, vous devez entrer un tableau supplémentaire qui servira de "cache" pour nos calculs: avant de calculer la nouvelle valeur, nous vérifierons si cela a été calculé auparavant. S'ils sont calculés, nous allons prendre une valeur à l'emploi du tableau et, s'il n'est pas calculé - vous devrez le considérer sur la base des précédents et mémoriser pour l'avenir:

Au cache; int fibo (int n) (si (cache [n] \u003d\u003d 0) (si (n \u003d\u003d 1 1 || n \u003d\u003d 2) (cache [n] \u003d 1;) Autres (cache [n] \u003d fibo (n] - 1) + fibo (n-2);)) renvoyer le cache [n];)

Depuis dans cette tâche pour calculer la valeur N-Mind, nous serons garantis pour être garantis (N-1) -E, il ne sera pas difficile de réécrire la formule à une forme itérative - nous remplirons simplement notre tableau dans un rangée jusqu'à ce qu'il s'agisse de la cellule désirée:

<= n; i++) { cache[i] = cache + cache; } cout << cache;

Maintenant, nous pouvons remarquer que lorsque nous calculons la valeur F (n), la valeur F (N-3) est déjà garantie jamais n'aura pas besoin. C'est-à-dire qu'il nous suffit de stocker seulement deux valeurs en mémoire - F (N-1) et F (N-2). De plus, dès que nous avons calculé F (n), le stockage F (N-2) perd tout sens. Essayons d'écrire ces réflexions sous forme de code:

// deux valeurs précédentes: int cache1 \u003d 1; int cache2 \u003d 1; // nouvelle valeur int cache3; pour (int i \u003d 2; i<= n; i++) { cache3 = cache1 + cache2; //Вычисляем новое значение //Абстрактный cache4 будет равен cache3+cache2 //Значит cache1 нам уже не нужен?.. //Отлично, значит cache1 -- то значение, которое потеряет актуальность на следующей итерации. //cache5 = cache4 - cache3 => Par l'itération perdra la pertinence de la cache2, c'est-à-dire Il devrait s'agir de cache1 // en d'autres termes, cache1 - F (N-2), cache2 - F (n-1), cache3 - F (N). // let n \u003d n + 1 (le numéro que nous calculons dans la prochaine itération). Ensuite, N-2 \u003d N-3, N-1 \u003d N - 2, N \u003d N-1. // conformément aux nouvelles réalités, nous réécrivons les valeurs de nos variables: cache1 \u003d cache2; cache2 \u003d cache3; ) COUT<< cache3;

Le programmeur expérimenté est clair que le code est supérieur, en général, non-sens, car la cache3 n'est jamais utilisée (elle est immédiatement enregistrée dans la cache2) et vous pouvez réécrire toute itération en utilisant une seule expression:

Cache \u003d 1; cache \u003d 1; pour (int i \u003d 2; i<= n; i++) { cache = cache + cache; //При i=2 устареет 0-й элемент //При i=3 в 0 будет свежий элемент (обновили его на предыдущей итерации), а в 1 -- ещё старый //При i=4 последним элементом мы обновляли cache, значит ненужное старьё сейчас в cache //Интуитивно понятно, что так будет продолжаться и дальше } cout << cache;

Pour ceux qui ne peuvent pas comprendre à quel point la magie fonctionne avec le résidu de la division ou veut simplement voir une formule plus évidente, il y a une autre solution:

Int x \u003d 1; int y \u003d 1; pour (int i \u003d 2; i< n; i++) { y = x + y; x = y - x; } cout << "Число Фибоначчи: " << y;

Essayez de suivre l'exécution de ce programme: vous serez sûr de corriger l'algorithme.

P.s. En général, il existe une seule formule pour calculer un nombre quelconque de fibonacci, qui ne nécessite aucune itération ni récursivité:

Const double sqrt5 \u003d sqrt (5); Const double phi \u003d (sqrt5 + 1) / 2; INT FIBO (INT N) (Retour Int (POW (PHI, N) / SQRT5 + 0.5);)

Mais comme vous pouvez le deviner, la capture est que le prix du calcul des degrés des nombres neuropaux est assez important, de même que leur erreur.

Les programmeurs du numéro de Fibonacci devraient déjà aimer. Des exemples de leurs calculs sont utilisés partout. Tout, du fait que ces chiffres fournissent l'exemple le plus simple de la récursion. Et ils sont un bon exemple de programmation dynamique. Mais est-il nécessaire de les calculer donc dans le vrai projet? Ne pas. Ni la récursion ni la programmation dynamique sont des options idéales. Et formule non fermée utilisant des nombres de points flottants. Maintenant, je vais vous dire comment correctement. Mais passez d'abord à travers toutes les solutions bien connues.

Le code est conçu pour Python 3, bien qu'il doit aller sur Python 2.

Pour commencer - je rappelle à la définition:

F n \u003d f n-1 + f n-2

Et f 1 \u003d f 2 \u003d 1.

Formule fermée

Manquons les détails, mais ceux qui veulons se familiariser avec la conclusion de la formule. L'idée est de supposer qu'il existe un certain X pour lequel f n \u003d x n, puis trouver x.

Quels moyens

Réduire x N-2

Nous résolvons l'équation carrée:

D'où la "section d'or" est en croissance \u003d (1 + √5) / 2. Substituer les valeurs initiales et avoir fait plus d'informatique, nous obtenons:

Comme nous utilisons pour calculer F n.

De __Future__ Division des importations Importation Math Math FIB (N): SQRT5 \u003d MATH.SQRT (5) PHI \u003d (SQRT5 + 1) / 2 RETURN INT (PHI ** N / SQRT5 + 0.5)

Bien:
Rapidement et juste pour la petite n
Pauvres:
Opérations de virgule flottante recherchées. Pour la grande n, une grande précision sera nécessaire.
Mal:
L'utilisation de nombres intégrés pour calculer F n est belle d'un point de vue mathématique, mais laid - avec un ordinateur.

Réursion

La décision la plus évidente que vous avez déjà vue plusieurs fois - probablement, comme exemple de quelle récursion est. Je le répète une fois de plus pour la complétude. En Python, il peut être enregistré en une seule ligne:

FIB \u003d Lambda N: FIB (N - 1) + FIB (N-2) Si N\u003e 2 Autres 1

Bien:
Mise en œuvre très simple répétant la définition mathématique
Pauvres:
Heure d'exécution exponentielle. Pour grand n très lentement
Mal:
Pile débordement

Mémoire

La solution avec récursivité a un gros problème: calculer les calculs. Lorsque FIB (N) est appelé, FIB (N-1) et FIB (N-2) sont calculés. Mais lorsque la FIB est considérée (N-1), elle calculera de manière indépendante FIB (N-2) - c'est-à-dire que la FIB (N-2) sera calculée deux fois. Si vous continuez les arguments, on verra que la FIB (N-3) sera calculée trois fois, etc. Trop d'intersections.

Par conséquent, il vous suffit de mémoriser les résultats afin de ne pas les compter à nouveau. Le temps et la mémoire de cette solution sont passés de manière linéaire. En résolvant, j'utilise un dictionnaire, mais vous pouvez utiliser un tableau simple.

M \u003d (0: 0, 1: 1) def fib (n): si n in m: renvoie m [n] m [n] m [n] \u003d fib (n-1) + fib (n-2) retour m [n]

(En python, il peut également être fait à l'aide d'un décorateur, functools.lru_cache.)

Bien:
Il suffit de transformer la récursion en une solution de mémorisation. Tournez le temps exponentiel pour exécuter en linéaire, pour lequel elle passe plus de mémoire.
Pauvres:
Passe beaucoup de mémoire
Mal:
Il est possible de déborder la pile, comme dans la récursivité

Programmation dynamique

Après la décision avec la mémorisation, il devient clair que nous n'avons pas besoin de tous les résultats précédents, mais seulement les deux derniers. De plus, au lieu de commencer par FIB (N) et retournez, vous pouvez commencer par FIB (0) et aller de l'avant. Le code suivant a une exécution de temps linéaire et l'utilisation de la mémoire est corrigée. En pratique, la vitesse de la solution sera encore plus élevée, car il n'y a pas de défis récursif de fonctions et de l'opération associée. Et le code semble plus facile.

Cette solution est souvent apportée comme exemple de programmation dynamique.

DEF FIB (N): A \u003d 0 B \u003d 1 pour __ dans la plage (n): A, B \u003d B, A + B Renvoyez un

Bien:
Fonctionne rapidement pour le petit code simple
Pauvres:
Temps d'exécution toujours linéaire
Mal:
Oui, rien n'est rien.

Matrice algèbre

Et enfin, la solution la moins éclairée, mais la solution la plus correcte, en utilisant le temps et la mémoire. Il peut également être étendu sur toute séquence linéaire homogène. Idée dans l'utilisation de matrices. C'est assez facile de voir que

Et la généralisation dit que

Deux valeurs pour X, obtenues par nous plus tôt, dont une cérémonie d'or, sont des valeurs propres de la matrice. Par conséquent, une autre façon de produire une formule fermée est l'utilisation d'une équation matricielle et d'une algèbre linéaire.

Alors, qu'est-ce qui est utile de ce libellé? Par le fait que l'exposition peut être effectuée pour le temps logarithmique. Cela se fait à travers la construction de la place. L'essentiel est que

Où la première expression est utilisée pour même une, la seconde pour impair. Il reste seulement d'organiser des multiplications des matrices et tout est prêt. Le code suivant est obtenu. J'ai organisé une mise en œuvre récursive de POW, car il est plus facile de comprendre. La version itérative regarde ici.

DEF POW (X, N, I, MULT): "" "Retourne x au degré n. Il suppose que je suis une matrice unique qui varie avec mul, et n est un ensemble positif" "" si n \u003d\u003d 0: retour I elif n \u003d\u003d 1: retour x else: y \u003d pow (x, n // 2, i, mul) y \u003d mul (y, y) si n% 2: y \u003d mul (x, y) retour y Identity_Matrix (n): "" "Retourne une matrice unique N sur N" "" R \u003d Liste (plage (n)) Retour [pour J in R] def matrix_multiphe (A, B): BT \u003d Liste (zip (* b )) Retour [pour Row_A dans A] DEF FIB (N): F \u003d POW ([,], N, Identity_Matrix (2), Matrix_Multivy) Retour F

Bien:
Mémoire fixe, heure logarithmique
Pauvres:
Le code est plus compliqué
Mal:
Avoir à travailler avec des matrices, bien qu'ils ne soient pas si mauvais

Comparaison de la vitesse

Ce n'est qu'une variante de programmation dynamique et de matrice. S'ils les comparent par le nombre de caractères, parmi n, il s'avère que la solution matricielle est linéairement et la solution avec une programmation dynamique est exponentielle. Exemple pratique - Calcul de FIB (10 ** 6), le nombre qui aura plus de deux cent mille caractères.

N \u003d 10 ** 6
Calculer FIB_MATRIX: FIB (N) ne comporte que 208988 chiffres, le calcul a pris 0,24993 secondes.
Calculer FIB_DYNAMIC: FIB (N) n'est que de 208988 chiffres, le calcul a pris 11,83377 secondes.

Commentaires théoriques

Ne touche pas directement le code donné ci-dessus, cette remarque est toujours un intérêt. Considérez le graphique suivant:

Calculez le nombre de chemins N à partir de A à B. Par exemple, pour N \u003d 1, nous en avons un moyen, 1. Pour N \u003d 2, nous avons à nouveau une solution, 01. Pour n \u003d 3, nous avons deux manières, 001 et 101 . Il est assez simple de montrer que le nombre de chemins n de A à B est égal à la précision F n. Après avoir écrit la matrice d'arrangement pour le graphique, nous obtenons la même matrice décrite ci-dessus. Il s'agit d'un résultat bien connu de la théorie des graphiques, qui pour une matrice donnée d'adjacence A, la survenue de C N est le nombre de chemins n dans la colonne (une des tâches mentionnées dans le film "Umnitsa chassera" ).

Pourquoi existe-t-il de telles désignations sur les erreurs? Il s'avère que lorsque vous envisagez une séquence infinie de caractères sur sans fin des deux côtés de la séquence des chemins de la colonne, vous obtiendrez quelque chose appelé «Type de type final», qui est un type de système de haut-parleurs symboliques. Plus précisément, ce type de type final est connu sous le nom de «décalage de la section dorée» et est défini comme un ensemble de «mots interdits» (11). En d'autres termes, nous obtiendrons des séquences binaires infinies dans les deux sens et aucune paire d'entre eux ne sera adjacente. L'entropie topologique de ce système dynamique est égale à la section dorée φ. Je me demande comment ce nombre apparaît périodiquement dans différents domaines de mathématiques.

NUMÉROS DE FIBONACCI - Il s'agit d'un certain nombre de chiffres dans lesquels chaque numéro suivant est égal à la somme des deux précédentes: 1, 1, 2, 3, 5, 8, 13, .... Parfois, une rangée commence à partir de zéro: 0, 1, 1, 2, 3, 5, .... Dans ce cas, nous adhérerons à la première option.

Formule:

F 1 \u003d 1
F 2 \u003d 1
F n \u003d f n-1 + f n-2

Exemple de calcul:

F 3 \u003d F 2 + F 1 \u003d 1 + 1 \u003d 2
F 4 \u003d F 3 + F 2 \u003d 2 + 1 \u003d 3
F 5 \u003d F 4 + F 3 \u003d 3 + 2 \u003d 5
F 6 \u003d F 5 + F 4 \u003d 5 + 3 \u003d 8
...

Calculer le N-ème numéro de la ligne Fibonacci en utilisant le cycle tandis que

1. Attribuez les premiers premiers éléments de la série aux variables FIB1 et FIB2, c'est-à-dire une unité à une variable.
2. Demandez le numéro d'utilisateur de l'élément dont il souhaite obtenir la valeur. Attribuer le numéro de variable n.
3. Effectuez les actions suivantes N - 2 fois, car les deux premiers éléments sont déjà pris en compte:
   1. Correction FIB1 et FIB2 en attribuant le résultat d'une variable pour le stockage temporaire des données, par exemple, FIB_SUM.
   2. Variable FIB1 attribue la valeur FIB2.
   3. Variable FIB2 Attribuez la valeur FIB_SUM.
4. Afficher la FIB2.

Noter. Si l'utilisateur entre 1 ou 2, le corps du cycle n'est jamais effectué, la valeur FIB2 d'origine est affichée.

fib1 \u003d 1 fib2 \u003d 1 n \u003d entrée () n \u003d int (n) i \u003d 0 pendant que je< n - 2 : fib_sum = fib1 + fib2 fib1 = fib2 fib2 = fib_sum i = i + 1 print (fib2)

Option de code compact:

fib1 \u003d fib2 \u003d 1 n \u003d int (entrée ( "Nombre d'éléments d'une rangée de fibonacci:")) - 2 tandis que N\u003e 0: FIB1, FIB2 \u003d FIB2, FIB1 + FIB2 N - \u003d 1 Imprimer (FIB2)

Sortie des numéros de Fibonacci avec un cycle pour

Dans ce cas, non seulement la valeur de l'élément de fondation d'une série de fibonacci est affichée, mais également tous les nombres à cela inclus. Pour ce faire, la sortie de la valeur FIB2 est placée dans le cycle.

fib1 \u003d fib2 \u003d 1 n \u003d int (entrée ()) si n< 2 : quit() print (fib1, end= " " ) print (fib2, end= " " ) for i in range (2 , n) : fib1, fib2 = fib2, fib1 + fib2 print (fib2, end= " " ) print ()

Exemple d'exécution:

10 1 1 2 3 5 8 13 21 34 55

Calcul récursif du N-ème numéro de la ligne Fibonacci

1. Si N \u003d 1 ou N \u003d 2, retournez à l'unité de branche d'appel, car les premier et second éléments de la gamme Fibonacci sont égaux à un.
2. Dans tous les autres cas, causer la même fonction avec les arguments N - 1 et N - 2. Le résultat de deux appels à plier et à revenir à la branche de l'appelant du programme.

dEF FIBONACCI (N): IF N IN (1, 2): Retour 1 Retour Fibonacci (N - 1) + Fibonacci (N - 2) Imprimer (Fibonacci (10))

Supposons n \u003d 4. Il y aura alors un appel récursif Fibonacci (3) et Fibonacci (2). La seconde retournera une unité et la première conduira à deux autres défis de la fonction: Fibonacci (2) et Fibonacci (1). Les deux appels seront retournés par un, dans le montant qu'il y aura deux. Ainsi, l'appel Fibonacci (3) renvoie le numéro 2, qui est résumée avec un numéro 1 de l'appel Fibonacci (2). Résultat 3 retourne à la branche principale du programme. Le quatrième élément de la gamme Fibonacci est trois: 1 1 2 3.