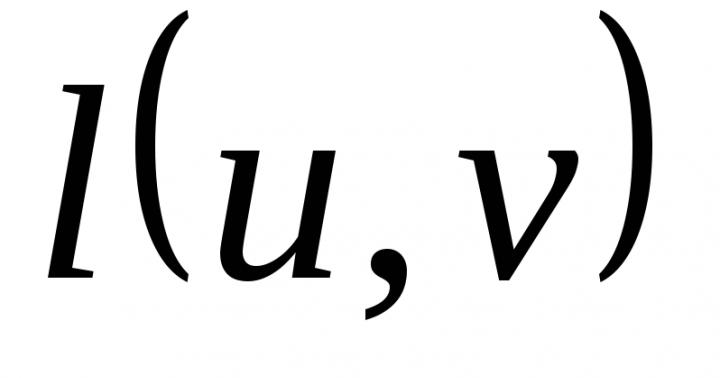Metodo Daekstra trova il percorso più breve. Grafici. Trovare la distanza più breve tra i due vertici usando l'algoritmo Deiquistra. Schema dell'algoritmo sequenziale

L'algoritmo Daekstra è un algoritmo sui grafici, che trova il percorso più breve tra i due vertici nel grafico con lunghezze non negative dell'arco. È anche spesso un compito di calcolare il percorso più breve da questo vertice a tutti gli altri. L'algoritmo è ampiamente utilizzato nella programmazione, ad esempio, viene utilizzato dai protocolli di routing.

Descrizione

L'ingresso dell'algoritmo viene somministrato un grafico orientato ponderato con archi di peso non negativi. L'uscita è un insieme di percorsi più corti da questo vertice ad altri.

All'inizio, si presume che la distanza per il vertice iniziale sia zero, e le distanze a tutti gli altri sono comprese infinite. Una serie di flag che denotano se la parte superiore è passata, piena di zeri. Quindi, ad ogni fase del ciclo, viene cercato una cima con una distanza minima verso l'iniziale e la bandiera uguale a zero. Per questo, la bandiera è installata e tutti i vertici vicini vengono controllati. Se la distanza precedente dal vertice sorgente viene precedentemente controllato rispetto alla quantità di distanza dal vertice corrente e la lunghezza della costola da esso al vertice selezionato, quindi la distanza dal vertice testato equivale alla distanza dalla corrente + bordo dalla corrente al corrente attualmente controllata. Il ciclo è completato quando le bandiere di tutti i vertici diventano uguali a 1 o quando la distanza da tutti i vertici con flag 0 è infinita. L'ultimo caso è possibile quindi e solo se il conteggio è intollerante.

Algoritmo Daekstra. in pseudocode.

Ingresso: A PARTIRE DAL : Array of Real - Count Arc Log Matrix; S è un vertice da cui il percorso più breve e T è un vertice a cui sta cercando.

Uscita: V\u003e Array del reale; e N: array di 0.... Se il top. v. Si trova nel percorso più breve da s. per t, quella TV]- Lunghezza del percorso più breve da s. per y; H [y] - Top, direttamente precedente w. Nel percorso più breve.

H è un array in cui il vertice n corrisponde al vertice m, il precedente sulla strada per n da s.

T è un array in cui il vertice n corrisponde alla distanza da esso a s.

X è un array in cui il vertice n corrisponde a 1 se il percorso è noto ad esso, e 0, se no.

inizializzazione degli array:

per v. da 1 a. r. fare.

T [v.]: = ∞ (il percorso più breve è sconosciuto)

X [V]: \u003d 0 (tutti i vertici non sono contrassegnati)

H [s]: \u003d 0 ( s. Niente precede)

T [s]: \u003d 0 (il percorso più breve ha una lunghezza di 0 ...)

X [s]: \u003d 1 (... ed è conosciuto) v. : = s. (Vertice corrente)

M: (segni di aggiornamento)

per e ∈. G ( e) fare

se X [e] = 0 & T [e]> TV] + C. Poi.

T [e]: = TV] + C. (un percorso più breve da s. nel e attraverso v. }

H [u]:= v. (ricordalo)

m.: = ∞

v. : = 0

(cerca la fine del percorso più breve)

per e da 1 a. p. fare.

se X [u] = 0 & T [u]< t. Poi.

v:= u.;

m:= T [u] (Superiore v. finisce il percorso più breve da s.

se v. = 0 allora.

sTOP (nessun percorso da s. nel t.) Finisci se

se v.= t. Poi.

fermarsi (il percorso più breve da s. nel t.) Finisci se

X [v]: \u003d 1 (il percorso più breve da s. nel v. ) Vai a. M.

Giustificazione

Per dimostrare la correttezza dell'algoritmo Daekstra, è sufficiente notare che con ogni esibizione del corpo del ciclo, che inizia l'etichetta M, come v.un vertice viene utilizzato per il quale è noto il percorso più corto dall'alto. s.In altre parole, se X [V] \u003d 1, quindi T [V] \u003d D (S, V) , E tutti i vertici sul sentiero (S, V), determinati dal vettore N, hanno la stessa proprietà, cioè

VU T [e] \u003d 1 \u003d\u003e T [e] \u003d D (S, U) & T] \u003d 1.

Davvero (per induzione), prima volta v. Il vertice S viene utilizzato per il quale il percorso più breve è vuoto e ha una lunghezza di 0 (percorsi non vuoti non possono essere più brevi, poiché la lunghezza degli archi non è negativa). Let t [u] \u003d d (s, u) per tutti i vertici precedentemente contrassegnati e. Considera il vertice appena segnato v.che è selezionato dalla condizione T [v] \u003d min T [e]. Si noti che se il modo è noto attraverso i vertici segnati, quindi è anche noto per il percorso più breve. Supponiamo (altrimenti), che T [v]\u003e D (S, V), cioè il percorso trovato da s.nel v,non è il più breve Poi ci dovrebbero essere vertici insignificanti su questo percorso. Considera il primo vertice w.su questo percorso, tale che T [W] = 0. IIM: T [W] = d (s, w) ⩽d (s\u003e v)< Т[v],что противоречит выбору вершины u.

Difficoltà temporanea

La complessità dell'algoritmo Daekstra dipende dal metodo di ricerca non visitato dalla parte superiore con una distanza minima dall'iniziale, metodo per la conservazione di una pluralità di vertici e metodi di aggiornamento dei tag. Sia n il numero di vertici e attraverso M - il numero di bordi nella colonna. Quindi, nel caso più semplice, quando tutti i vertici impostati vengono visualizzati per cercare i vertici con una distanza minima dal vertice iniziale, e un array viene utilizzato per memorizzare le distanze, il tempo di funzionamento dell'algoritmo - o (n 2). Il ciclo principale viene eseguito circa n volte, in ciascuno di essi, il minimo è speso per le operazioni n. Il numero di operazioni viene speso sui cicli lungo i vicini di ogni visita il vertice, il numero di robusto m (poiché ogni bordo si trova in questi cicli agevolmente due volte e richiede un numero costante di operazioni). Pertanto, il tempo di funzionamento generale dell'algoritmo O (N 2 + M), ma poiché M è inferiore a N (N-1), alla fine si scopre (n 2).

Per i grafici rarefatti (cioè, tale per cui M è molto meno di n²) i vertici non modificati possono essere memorizzati in un mucchio binario e come chiave per utilizzare le distanze. Poiché il ciclo viene eseguito circa n volte, e il numero di rilassamento (cambiamenti delle etichette) non è superiore a M, il tempo di funzionamento di tale implementazione - o (nlogn + mlogn)

Esempio

Calcolo delle distanze dal vertice 1 per i vertici passabili:

Prima di ogni area della città (se riesci a muoversi solo sulle strade).

Opzione 2. Ci sono alcuni voli tra le città del mondo, per ogni costo famoso. Il costo del volo da A a B potrebbe non essere uguale al costo del volo da B a A. Trova il percorso del costo minimo (possibilmente con i trasferimenti) da Copenaghen a Barnaul.

Definizione formale

Esempio

Considera l'esecuzione dell'algoritmo sull'esempio del grafico mostrato nella figura.

Lascia che sia necessario trovare la distanza più breve dal 1 ° Vertice a tutti gli altri.

Implementazione nei linguaggi di programmazione

Performance in Language C (SI)

#Define Dimensione 6 #Define INF 1000000000 INT A [Dimensioni] [Dimensione] \u003d ((INF, 5, INF, INF, INF, INF), (1, 2, 3, 4, 5, 6), // Matrix percorsi (1, 2, 3, 4, 5, 6), (1, 2, 3, 4, 5, 6), // indici orizzontali dal punto { 1 , 2 , 3 , 4 , 5 , 6 },{ 1 , 2 , 3 , 4 , 5 , 6 }}; // verticale al punto, valore - peso Int d [dimensione]; // array dei percorsi più corti trovati, indici - vertici del grafico void deikstra () (int v [dimensione]; // array di etichette int temp, i; int minindex, min; per (i \u003d 0; io< SIZE ; i ++ ) { d [ i ] = INF ; // array di percorsi è inizializzato l'infinito v [i] \u003d 1; ) D [0] \u003d 0; fare ( // Esecuzione dell'algoritmo minindex \u003d inf; Min \u003d inf; per (i \u003d 0; io< SIZE ; i ++ ) { if ((v [ i ] == 1 ) && (d [ i ] < min )) { min = d [ i ]; minindex = i ; } } if (minindex != INF ) { for (i = 0 ; i < SIZE ; i ++ ) { if (a [ minindex ][ i ] > 0) (temp \u003d min + a [minindex] [i]; se (temp< d [ i ]) d [ i ] = temp ; } } v [ minindex ] = 0 ; } } while (minindex < INF ); }

percorso più breve Oggi è un compito vitale e viene utilizzato quasi ovunque, che spazia dal trovare la rotta ottimale tra due oggetti sul terreno (ad esempio, il percorso più breve da casa all'università), nei sistemi di autopilota, per trovare il percorso ottimale durante il trasporto, Pacchetto di commutazione delle informazioni in reti e T.P.

Il percorso più breve è considerato utilizzando un determinato oggetto matematico chiamato grafico. Ricerca percorso più breve È condotto tra due vertici specificati nel grafico. Il risultato è il percorso, cioè la sequenza di vertici e costole, incidente per i due vertici vicini e la sua lunghezza.

Considerare tre la maggior parte algoritmo efficace Posa percorso più breve:

• algoritmo Daekstra.;
• Algoritmo floyd;
• algoritmi overborn.

Questi algoritmi sono facilmente eseguiti con un piccolo numero di vertici nel grafico. Con un aumento del loro numero di attività di ricerca percorso più breve Completare.

Algoritmo Daekstra.

Questo algoritmo è un algoritmo sui grafici, che è stato inventato dallo scienziato olandese E. Dyakstroy nel 1959. L'algoritmo trova la distanza più breve da uno dei vertici del grafico a tutti gli altri e funziona solo per i grafici senza costole di peso negativo.

Ogni vertice è attribuito al peso - questo è il peso del percorso dal vertice iniziale a questo. Inoltre, ogni vertice può essere evidenziato. Se il vertice è evidenziato, il percorso da esso al vertice iniziale è il più breve, se non, quindi temporaneo. Venendo dal grafico, l'algoritmo considera il percorso per ogni vertice e, se risulta essere il più breve, evidenzia la cima. Il peso di questo vertice è il peso del percorso. Per tutti i vicini di questo vertice, l'algoritmo calcola anche il peso, senza circostanze che li usano in qualsiasi circostanza. L'algoritmo finisce il suo lavoro, raggiungendo il vertice finale e la pesatura percorso più breve Il peso del vertice finale diventa.

Algoritmo Daekstra.

Passaggio 1. A tutti i piani, ad eccezione del primo, il peso è assegnato un'infinito uguale e il primo vertice è 0.

Passaggio 2. Tutti i vertici non sono evidenziati.

Passaggio 3. Il primo vertice è dichiarato corrente.

Passaggio 4. Il peso di tutti i vertici non corrisposti è tradotto dalla formula: il peso del vertice non definito è il numero minimo del vecchio peso di questo vertice, la quantità del peso del vertice corrente e il peso del bordo che collega il bordo Vertice corrente con il non decisore.

Passaggio 5. Tra i picchi non definiti è un top con peso minimo. Se questo non è stato trovato, cioè il peso di tutti i vertici è uguale all'infinito, il percorso non esiste. Di conseguenza, l'uscita. Altrimenti, la corrente è la parte superiore risultante. È assegnato.

Passaggio 6. Se il vertice corrente risulta essere il finale, il percorso è stato trovato e il suo peso è il peso del vertice finale.

Passaggio 7. Vai al passaggio 4.

Nell'attuazione del software algoritmo Daekstra. Costruiremo una serie di vertici s per i quali sono già noti i percorsi più brevi del vertice iniziale. Ad ogni passaggio al set S, viene aggiunto lo stesso vertice, la distanza dal vertice iniziale è inferiore a per altri vertici rimanenti. In questo caso, useremo l'array D, in cui sono registrate le lunghezze percorsi più corti Per ogni vertice. Quando il set S contiene tutti i vertici del grafico, quindi l'array d conterrà lunghezze percorsi più corti Dal vertice iniziale a ciascun vertice.

Oltre agli array specificati, utilizzeremo la matrice C di C, dove l'elemento C è la lunghezza dei bordi (I, J), se non ci sono costine, la sua lunghezza è affidata a un'infinito uguale, cioè, cioè più di ogni lunghezza effettiva della nervatura. In realtà matrix c è matrice di navigazionein cui tutti gli elementi zero sono sostituiti con l'infinito.

Per determinare lo stesso

5.4.3. La sfida del percorso più corto e del algoritmo di Daekster della sua decisione

Lascia che il set di orgraf G.(V., E.), con ogni arco di cui è messo in linea con il numero
chiamato arc Long..

Definizione. Lena. Il percorso è chiamato la somma delle lunghezze dell'arco che compongono questa strada. Il compito del percorso più brevemette così.

Opzione 1. Trova le lunghezze dei percorsi più brevi (modi di lunghezza minima) e dei percorsi stessi dal vertice fisso s. a tutti gli altri vertici del grafico.

Opzione 2. Trova le lunghezze dei percorsi più corti e dei percorsi tra tutte le coppie dei vertici di questo grafico.

Se ci sono archi negativi nella colonna, l'attività potrebbe non avere soluzioni (perderà il significato). Ciò è dovuto al fatto che il contorno della lunghezza negativa può essere presente nella colonna. La presenza di circuiti di lunghezza negativa significa che la lunghezza del percorso può essere effettuata uguale
. E se non ci sono circuiti di lunghezza negativa, i percorsi più brevi esistono e qualsiasi percorso più breve è una catena semplice.

Si noti che se il percorso più corto esiste, uno di esso è, è anche il percorso più breve tra i rispettivi vertici.

Algoritmo Daekstra risolve il problema del percorso più breve.

L'algoritmo funziona con archi di lunghezza positiva e definisce i percorsi più corti dal vertice fisso s. a tutti gli altri vertici del grafico. Dennare questi vertici v. 1 , v. 2 ,…, v. n. .

Definizione. Chiamiamo la cima u. sdraiato più vicino all'inizio s.che top. v.Se la lunghezza del percorso più breve da s. prima u. meno della lunghezza del percorso più breve da s. prima v.. Diremo che le cime u. e v. equamente dall'alto s.Se le lunghezze dei percorsi più corti da s. prima u. e da s. prima v. abbinare.

L'algoritmo Daekstra razionalizza costantemente i vertici del grafico nel senso della prossimità in alto s. e in base ai seguenti principi di base.

Se le lunghezze dell'arco sono numeri positivi, allora

k. s. top - lei stessa. Lunghezza del percorso più breve da s. prima s. uguale a 0;

k. s. vertice s., Bugie da. s. Alla distanza di un arco  il più breve di tutti gli archi lasciando la cima s.;

qualsiasi parte superiore intermedia del percorso più breve da s. Ad alcuni vertici v. Si avvicina a K. s.del vertice finale v.;

il percorso più breve per il prossimo vertice ordinato può passare solo attraverso picchi già ordinati.

Lascia che l'algoritmo abbia già ordinato le cime v. 1 , v. 2 … v. k. . Dentare entro
,
La lunghezza del percorso più corto verso l'alto v. iO. .

Considera tutti gli archi del grafico sorgente che iniziano in uno dei vertici del set.
E termina in altri vertici non ordinati. Per ogni tale arco, per esempio
, Calcola la somma
. Questo importo è uguale alla lunghezza del percorso da s. nel y.in cui il vertice v. iO. C'è un penultimo superiore e il percorso da s. nel v. iO. - il più breve di tutti i percorsi che si collegano s. e v. iO. .

Questa è la lunghezza più definita di tutti i percorsi da s. I picchi non ancora ordinati in cui sono solo i vertici sono i vertici intermedi k. K. s.. Lascia che il più breve di questi percorsi finisca in cima w.. Poi w. ed è
Per vicinanza a K. s. vertice.

Le azioni tecnicamente sull'algoritmo Daekstra vengono eseguite utilizzando l'apparato di marcatura VertX. Tag Verth. v. denota come
. Qualsiasi etichetta è un numero uguale alla lunghezza di qualche percorso da s. prima v.. I tag sono suddivisi in temporanei e costanti. Ad ogni passo, solo un'etichetta diventa costante. Ciò significa che il suo valore è uguale alla lunghezza del percorso più breve per il vertice corrispondente, e questo vertice stesso viene ordinato. Il numero del prossimo vertice ordinato è denotato dalla lettera r..

Descrizione dell'algoritmo.

Passo 1. (Installazione iniziale). Mettere
E considera questa costante di questa etichetta. Mettere
,
E considera questi segni temporanei. Mettere
.

Passo 2. (Passo condiviso). Lui ripete n. una volta ordinati tutti i vertici del grafico.

Ricalcolare un segno temporaneo
Tutti i vertici disordinati v. iO. che include un arco che lasciava la cima r, Per regola

Seleziona Top con un'etichetta minima del tempo. Se ci sono molti tali vertici, scegli qualsiasi.

Lascia che sia. w.- Top con un'etichetta minima. Prendere un'etichetta
costante e messo
.

I gradini dell'algoritmo Daekstra sono convenientemente redatti nella tabella, ogni colonna di cui corrisponde al vertice del grafico. Le righe del tavolo corrispondono alla ripetizione del passo complessivo.

Esempio. Per grafico in fig. 4. Trova i percorsi più brevi dei vertici
a tutti gli altri vertici del grafico. Le costole significano due archi multicidirezionali della stessa lunghezza.

Decisione. Nella scheda. 1 tag vertice registrati ad ogni passo. I tag permanenti sono contrassegnati con "+". Descriviamo in dettaglio come vengono calcolati i tag.

Dal Vertex 1 gli archi si affacciano sui vertici 2, 5, 6. Ricordando le etichette di questi vertici e riempire la seconda stringa della tabella.

La parte superiore del vertice 6 diventa costante,
.

Dal vertice 6 archi sono ancora i vertici non ordinati 2, 5, 8, 9. Ricalcolano i loro tag temporali

Riempi 3 file della tabella. Il minimo delle etichette del tempo è 3 (Top tag 9),
.

Dai vertice 9 archi in vertici ancora non ordinati 5, 8, 11, 12. Quindi

Riempire la quarta linea del tavolo. In questa linea, due vertici  2 e 12 hanno tag temporali minimi pari a 4. Primo ordine, ad esempio, il vertice 2. Quindi la parte superiore 12 verrà ordinata al passaggio successivo.

Tabella 1

Così,
.

Dalla top 2 ci sono archi in vertici ancora disordinati 3, 4, 5. Ricordando i segni temporanei di questi vertici

Compila 5 righe di tabella. Le etichette minime di tempo sono 4 (vertice tag 12),
.

Riempi 6 file della tabella. Le etichette minime di tempo sono 5 (Top tag 5),
.

Riempi 7 stringa del tavolo. Diventare un tag costante del vertice 8 (è uguale a 5),
.

Top 11 è ordinato.

Dal vertice 11 archi in vertici disordinati 7, 10. Ricordando i segni di tempo di questi vertici.

La top 4 ottiene un tag costante.

Dai vertice 4 archi nei vertici non ordinati 3, 7. Tag temporali di ricalcolo

Organizza il vertice 3.

Riempi 12 righe di tabella. A questo punto, ordiniamo l'ultimo vertice disordinato 10.

Costruire un albero di percorsi più corti.

L'albero dei percorsi più corti è un albero focalizzato con una radice nella parte superiore S. . Tutti i percorsi in questo albero sono il più breve per questo grafico.

L'albero del percorso più breve si basa sul tavolo, la parte superiore è accesa sopra il vertice nell'ordine in cui hanno ricevuto tag costanti. Il primo nell'albero attiva la radice - il vertice S. .

Costruiamo il modo più breve per il nostro esempio.

Innanzitutto, attiriamo la radice nell'albero - il vertice 1. Quindi l'arco è trasformato in un albero (1.6). Il prossimo è stato ordinato il vertice 9, la durata del percorso più breve a cui è uguale a 3. La prima volta il numero 3 è apparso nella terza linea, che è stata riempita con
. Di conseguenza, il vertice 6 è il penultimo top del percorso più breve per il vertice 9. Accendiamo la lunghezza del legno ARC (6.9) 1.

La Top 2 è stata ordinata con la lunghezza del percorso più breve pari a 4. Questo numero per la prima volta è apparso nella terza linea, che è stato riempito
. Di conseguenza, il percorso più breve nel secondo vertice passa lungo l'arco (6.2). Accendiamo l'arco (6.2) della lunghezza 2.

Il prossimo è stato ordinato il top 12,
. La prima volta il numero 4 appare nella quarta linea, che è stata riempita con
. L'albero include un arco (9.12) di lunghezza 1. L'albero totale dei percorsi più corti è mostrato in Fig. cinque.

L'algoritmo deiilandese può essere sbagliato se ci sono archi negativi nella colonna. Quindi, cercando i percorsi più corti dall'alto s. \u003d 1 per grafico in fig. 6, l'algoritmo ha ordinato per la prima volta il vertice 3, quindi il vertice 2 e finisce il lavoro. In questo caso, questo percorso più breve verso i primi 3, dal punto di vista dell'algoritmo di Daekstra,  è una lunghezza ARC (1.3) 3.

Infatti, il percorso più breve per il vertice 3 è costituito da archi (1.2) e (2.3), la lunghezza di questo percorso è 5 + (- 3) \u003d 2.

A causa della presenza di un arco (2.3) di una lunghezza negativa -3, i seguenti principi di base sono stati disturbati:

k. s. Il picco sta da esso ad una distanza di due archi, e non uno;

la parte superiore intermedia del percorso più breve 1-2-3 (Vertex 2) si trova ulteriormente dal vertice 1 (a una distanza di 5) rispetto al vertice finale del percorso 3.

Di conseguenza, la presenza di ARC di lunghezza negativa complica la soluzione del problema del percorso più breve e richiede l'uso di algoritmi più complessi, piuttosto che l'algoritmo Daekstra.

Risolvi il compito di trovare il percorso più breve dell'algoritmo di Daekstra.
Trova il percorso più breve da x0 a x7. Il conteggio è impostato dagli elementi della matrice di costo

Costruire questo grafico


Iniziamo con l'elemento x0 e lo assegniamo un tag 0, considera tutti i suoi vicini, perché Non c'è ancora nessuna nota, gli assegni le lunghezze corrispondenti:


Tutti i vicini X0 sono considerati, segniamolo e andiamo in cima a x1. I suoi vicini X0, X2, X4, ma X0 hanno segnato, non considerarlo. Per x2: , Lascia l'etichetta.

Per x4: Sostituendo l'etichetta. Tutti i vicini del Vertex X1 sono considerati, lo segniamo


Vai in cima a x2. I suoi vicini X0, X1, X3, X4, X5, X6, ma X0, X1 sono contrassegnati, non considerarli.
Per x3: , Lascia l'etichetta.
Per x5: Sostituendo l'etichetta.
Per x4: , Lascia l'etichetta.
Per x6: Sostituendo l'etichetta.
Sono considerati tutti i vicini della cima del X2, lo segniamo.


Vai al top x3. I suoi vicini X0, X2, X6, ma X0, X2 sono contrassegnati, non considerarli.
Per x6: , Lascia l'etichetta.
Tutti i vicini della cima della X3 sono considerati, lo segniamo.


Vai in cima a x4. I suoi vicini X1, X2, X5, X7, ma X1, X2 sono contrassegnati, non considerarli.
Per x5: Sostituendo l'etichetta.
Per x7: Sostituendo l'etichetta.
Sono considerati tutti i vicini della cima della x4, lo segniamo.


Vai all'inizio di x5. I suoi vicini X2, X4, X6, X7, ma X2, X4 sono contrassegnati, non considerarli.
Per x6: , Lascia l'etichetta.
Per x7: , Lascia l'etichetta.
Sono considerati tutti i vicini della cima del X5, lo segniamo.


Vai in cima a x6. I suoi vicini X2, X3, X5, X7, ma X2, X3, X5 sono contrassegnati, non considerarli.
Per x7: , Lascia l'etichetta.
Sono considerati tutti i cimiti della cima della X6, lo segniamo. E abbiamo etichettato il restante X7, sono considerati tutti i vertici.


Conclusione: il percorso più breve del loro X0 in X7 ha una lunghezza di 101, questo percorso: X7-X4-X1-X0.