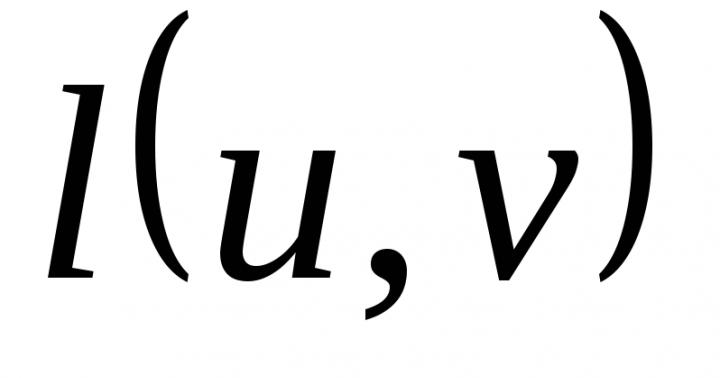W ubiegłym wieku Ivan Bernoulli, Leonard Euler, a następnie Jean-Batist Fourier po raz pierwszy zastosował prezentację okresowych funkcji z wierszami trygonometrycznych. Ta prezentacja jest szczegółowo badana w innych kursach, więc przypomnimy tylko główne relacje i definicje.

Jak zauważono powyżej, cała okresowa funkcja u (t) Dla której przeprowadza się równość u (t) \u003d u (t + t) gdzie T \u003d 1 / f \u003d 2p / W , Możesz sobie wyobrazić blisko Fouriera:

Każda kategoria tej serii może być rozkładana przez Cosinus Formuła dla różnicy w dwóch kątach i prześlij w formie dwóch terminów:

,

gdzie: A n \u003d c n cosφ n, b n \u003d c n sinφ n , tak , ale

Czynniki N. i Zajazd. zdefiniowane zgodnie z formułami EULER:

;
.

Dla n \u003d 0. :

ale B 0 \u003d 0.

Czynniki N. i Zajazd. są średnie wartości pracy funkcji u (t) i oscylację harmoniczną z częstotliwością pÓŁNOCNY ZACHÓD. w przedziale trwałości T. . Wiemy już (sekcja 2.5), że są to funkcje wzajemnej korelacji, która określa miarę ich połączenia. W konsekwencji współczynniki N. i B n. Pokaż nam "Ile sinusoidów lub cosinonów z częstotliwością pÓŁNOCNY ZACHÓD. zawarte w tej funkcji u (t) podzielony na rząd Fouriera.

W ten sposób możemy przedstawić okresową funkcję u (t) W formie sumy oscylacji harmonicznych, gdzie liczby C N. są amplitudy i liczby Φ N. - fazy. Zwykle w literaturze nazwał spektrum amplitudów i - Spektrum fazy. Często rozważa się tylko spektrum amplitudów, która jest przedstawiona w formie linii znajdujących się w punktach. pÓŁNOCNY ZACHÓD. na osi częstotliwości i o wysokości odpowiadającej liczbie C N. . Należy jednak pamiętać, że uzyskanie jednoznacznej korespondencji między funkcją czasu u (t) I jego widmo musi korzystać z widma amplitudowych i widma fazy. Jest to widoczne z takiego prostego przykładu. Sygnały będą miały taki sam spektrum amplitudów, ale zupełnie inny rodzaj funkcji czasowych.

Dyskretne widmo może mieć nie tylko okresową funkcję. Na przykład sygnał: nie jest okresowy, ale ma dyskretny spektrum składający się z dwóch linii widmowych. Będzie również ściśle okresowy sygnał składający się z sekwencji impulsów radiowych (impulsów z napełnianiem wysokiej częstotliwości), w którym okres następującego jest stała, ale początkowe faza napełniania wysokiej częstotliwości zmiany z pulsu do pulsu według impulsu do dowolnego prawa. Takie sygnały nazywane są prawie okresowe. Jak zobaczymy w przyszłości, mają również dyskretne widmo. Badanie fizycznego charakteru widm takich sygnałów, wykonamy tak samo jak okresowe.

Formy nagrywania serii Fouriera. Sygnał jest nazywany okresowyjeśli jego forma jest cyklicznie powtarzana w czasie okresowym sygnałem u (t)ogólnie jest napisany:

u (t) \u003d u (t + mt), m \u003d 0, ± 1, ± 2, ...

Tutaj okres sygnału. Sygnały okresowe mogą być proste i złożone.

Do matematycznej reprezentacji sygnałów okresowych z okresem T.często używaj w pobliżu (2.2), w którym harmoniczne (sinusoidalne i cosines) oscylacje są wybierane jako podstawowe funkcje

y 0 (t) \u003d 1; y 1 (t) \u003d sinw 1 t; y2 (t) \u003d cosw 1 t;

y3 (t) \u003d sin2w 1 t; y 4 (t) \u003d cos2w 1 t; ..., (2.3)

gdzie W 1 \u003d 2P / T - główna częstotliwość kątowa sekwencji

funkcje. Z harmonicznych podstawowych funkcji z liczby (2.2) otrzymujemy szereg Fourier (Jean Fourier - Francuski matematyk i fizyka XIX wieku).

Funkcje harmoniczne formularza (2.3) w wielu fourier ma następujące zalety: 1) prosty opis matematyczny; 2) niezmienność do transformacji liniowych, tj. Jeśli wejście obwodu liniowego obsługuje oscylację harmoniczną, a następnie przy jego wylocie będzie również oscylację harmoniczną, różniącą się od wejścia tylko amplitudy i fazę początkową; 3) jako sygnał, funkcje harmoniczne są okresowe i mają nieskończony czas trwania; 4) Technika do generowania funkcji harmonicznych jest dość prosta.

Od oceny matematycznej wiadomo, że rozkładając sygnał okresowy w rzędzie dla funkcji harmonicznych (2.3), konieczne jest wykonanie warunków derichle. Ale wszystkie prawdziwe sygnały okresowe są zadowoleni z tych warunków i mogą być reprezentowane jako seria Fouriera, która może być rejestrowana w jednej z następujących form:

u (t) \u003d 0/2 + (A 'MN COSNW 1 T + A "MN NW 1 t), (2.4)

gdzie są współczynniki

A mn "\u003d (2.5)

u (t) \u003d 0/2 + (2.6)

A mn \u003d. (2.7)

lub w złożonej formie

u (t) \u003d (2.8)

C n \u003d (2.9)

Z (2.4) - (2.9) Wynika z tego, że w ogólnym przypadku okresowy sygnał U (t) zawiera stały składnik 0/2 i zestaw oscylacji harmonicznych częstotliwości głównej W 1 \u003d 2PF 1 i jego harmoniczne z częstotliwościami WN \u003d NW 1, N \u003d 2, 3.4, ... Każda z harmonicznych

oscylacje serii Fouriera charakteryzują się amplitudem początkowej fazy Y n .nn

Diagram widmowy i widmo sygnału okresowego. Jeśli jakikolwiek sygnał jest reprezentowany jako suma oscylacji harmonicznych o różnych częstotliwościach, to mówią to rozkład widmasygnał.

Diagram widmowy.sygnał nazywa się graficzną reprezentacją współczynników serii Fouriera tego sygnału. Są diagramy amplitudy i fazy. Na rys. 2.6 W pewnej skali, oś pozioma jest przełożona wartości częstotliwości harmonicznej, wzdłuż mallastycznej osi - ich amplitudy MN i fazę y n. Ponadto amplitudy harmoniczne mogą przyjmować dodatnie wartości, fazy - zarówno wartości pozytywne, jak i ujemne w przedziale -P £ y n £ p

Widmo sygnalizacyjne.- Jest to kombinacja składników harmonicznych o określonych wartościach częstotliwości, amplitudów i fazach początkowej tworzących sygnał w ilości. W zastosowaniach technicznych w praktyce, diagramy widmowe nazywane są bardziej krótkie - spektrum amplitudy, widmo fazowe.Najczęściej zainteresowany diagramem widmowym amplitudy. Można go oszacować przez odsetek harmonicznych w widmie.

Przykład2.3. Wysyłaj okresową sekwencję okresową prostokątnych impulsów wideo zsłynne parametry. (U, t, t z),nawet "w stosunku do punktu t \u003d 0. Aby skonstruować schemat widmowy amplitudów i faz w U M \u003d 2B, T \u003d 20ms, S \u003d T / T i \u003d 2 i 8.

Określony okresowy sygnał w przedziale jednego okresu może być zapisany jako

Używamy do reprezentowania tej formy sygnału nagrywania serii Fouriera wformularz (2.4). Ponieważ sygnał jest nawet, a następnie tylko cosonośnie pozostaną w rozkładzie.

Figa. 2.6. Spektralne okresowe wykresy sygnałowe:

a - amplituda; b.- faza

Integralny z funkcji nieparzystej na okres ravey zero. Według formuł (2.5) znajdziemy współczynniki

umożliwienie napisania serii Fouriera:

Aby skonstruować diagramy widmowe o określonych danych numerycznych, można zapytać \u003d 0, 1, 2, 3, ... i obliczyć współczynniki harmoniczne. Wyniki obliczenia pierwszych ośmiu składników widma są podsumowane w tabeli. 2.1. W liczbie (2.4) A "mn \u003d 0i według (2,7) MN \u003d | A 'MN |, główna częstotliwość F 1 \u003d 1 / t \u003d 1/20-10 -3 \u003d 50 Hz, W 1 \u003d 2pf 1 \u003d 2P * 50 \u003d 314rad / s. Spektrum amplitudy na rys.

2.7 Zbudowany dla takich n,dla którego I Mn.więcej niż 5% wartości maksymalnej.

Z powyższego przykładu 2.3 wynika z tego, że wraz ze wzrostem obowiązku liczba komponentów widmowych wzrasta, a ich amplitudy spadają. Mówi się, że taki sygnał ma bogate widmo. Należy zauważyć, że dla wielu praktycznie stosowanych sygnałów nie ma potrzeby obliczania amplitudy i faz harmonicznych zgodnie z poprzednimi formułami.

Tabela 2.1. Składniki amplitudy serii czterocznej sekwencji okresowej prostokątnych impulsów

Figa. 2.7. Diagramy widmowe w okresowej sekwencji impulsów: ale- Mocne strony S-2; - B-at Duty S \u003d 8

W katalogach matematycznych znajdują się rozkłady sygnałów z rzędu Fouriera. Jedna z tych tabel jest pokazana w dodatku (tabela. § 2).

Często pojawia się pytanie: ile wziąć spektralne ustawienia (harmoniczne), aby przedstawić prawdziwy sygnał obok Fouriera? Przecież liczba, ściśle mówiący, niekończący się. Nie można uzyskać tutaj jednoznacznej odpowiedzi. Wszystko zależy od formy sygnału i dokładności prezentacji w pobliżu Fouriera. Bardziej płynna zmiana sygnału - harmoniczna jest mniej wymagana. Jeśli sygnał ma skoki (przerwy), konieczne jest podsumowanie większej liczby harmonicznych, aby osiągnąć ten sam błąd. Jednak w wielu przypadkach, na przykład, w telegrafie, wierzą, że do przenoszenia prostokątnych impulsów z stromymi frontami jest wystarczająca ilość trzech harmonicznych.

Zajęcia dotyczące analizy matematycznej

Przedmiot: Liczenie kwot częściowych i charakterystyki widmowej serii Fouriera dla wyraźnej funkcji

funkcja Funkcja Spectrum Signal Fourier

1. Model procesu fizycznego

Rozwiązanie problemu z obliczeniami teoretycznymi

Przykład rozwiązania problemu

Przykład rozwiązania zadania w Matlab R2009A

Bibliografia

1. Model procesu fizycznego

Model matematyczny Technologia radiowa może służyć pewnej funkcji czasu fA.(t) . Ta funkcja może być prawdziwa lub złożona, jednowymiarowa lub wielowymiarowa, deterministyczna lub losowa (sygnały z zakłóceniami). W inżynierii radiowej, to samo model matematyczny Równy sukces opisuje prąd, napięcie, napięcie pole elektryczne itp.

Rozważ prawdziwe jednowymiarowe deterministyczne sygnały

Zestawy funkcji (sygnały) są zwyczajowe, które są uważane za liniowe normalizowane przestrzenie, w których wprowadzono następujące koncepcje i aksjomaty:

) Wszystkie aksjomaty powierzchni liniowej są wykonane;

) Produkt skalarny dwóch ważnych sygnałów jest zdefiniowany w następujący sposób:

) Dwa sygnały nazywane są ortogonalem, jeśli ich produkt skalarny wynosi zero;

) System sygnałów ortogonalnych tworzy nieskończoną podstawę współrzędnych, dla których można rozłożyć każdy okresowy sygnał należący do przestrzeni liniowej;

Wśród różnych systemów funkcji ortogonalnych, które można rozłożyć, system funkcji harmonicznego (sinusoidalne i cosinus) jest najczęstsze:

Reprezentacja określonego okresowego sygnału w postaci suma oscylacji harmonicznych o różnych częstotliwościach nazywana jest przedstawicielstwem widmowym sygnału. Oddzielne składniki harmoniczne sygnału stanowią spektrum. Z punktu widzenia matematycznego reprezentacja widmowa jest równoważna rozkładu okresowej funkcji (sygnału) w serii Fouriera.

Wartość rozkładu widmowego funkcji w inżynierii radiowej wynika z wielu powodów:

) Łatwy do zbadania właściwości sygnału, ponieważ Funkcje harmoniczne są dobrze badane;

) Możliwość generowania dowolnego sygnału, ponieważ Technika do generowania sygnałów harmonicznych jest dość prosta;

) prostota sygnału transmisji i odbioru przez kanał radiowy, ponieważ Oscylacja harmoniczna jest jedyną funkcją czasu, który zachowuje swój kształt podczas przechodzenia przez dowolną łańcuch liniowy. Sygnał na wylocie łańcucha pozostaje harmonicznie o tej samej częstotliwości, tylko amplituda i początkowej fazie zmiany oscylacji;

) Rozkład sygnału zatokowego i Cosine umożliwia korzystanie z symbolicznej metody zaprojektowanej do analizy transferu oscylacji harmonicznych przez łańcuchy liniowe.

Jako model procesu fizycznego uważamy elektrokardiogram serca serca.

2. Problem z obliczeniami teoretycznymi

Zadanie 1:

Opisujemy z serią Fouriera, okresowo powtarzający się puls na działce elektrokardiogramu, tzw. Kompleks QRS.

Kompleks QRS można ustawić według następujących fragmentarycznych funkcji liniowych.

Gdzie

Ta cecha może trwać okresowo z okresem T \u003d 2l..

Funkcje serii Fouriera:

Definicja 1.: Funkcja jest nazywana stały ciągły W segmencie [A, B], jeśli jest ciągły we wszystkich punktach tego segmentu, z wyjątkiem skończonej liczby punktów, w których istnieją swoje ostateczne limity jednostronne.

Definicja 2:Funkcja jest nazywana fragmentaryczne gładkie W pewnym segmencie, jeśli się sama i jej pochodna stała.

Twierdzenie 1 (znak Dirichleta): Fourier Row fragment fragmentarycznego w funkcji cięcia f (x.) Zbiega się w każdej ciągłości punktu do wartości funkcji w tym momencie i do wartości w każdym punkcie przerwy.

Nasza funkcja spełnia warunki twierdzenia.

Dla danej funkcji otrzymujemy następujące współczynniki serii Fouriera:

Złożona forma Fouriera

Aby reprezentować liczbę w kompleksowej formie, użyjemy formuł Eulera:

Wprowadzamy notację:

Wtedy liczba może być przepisana w formularzu

Ponadto współczynniki kompleksowej serii Fouriera można uzyskać bezpośrednio, obliczając je o wzorze

Piszemy w kompleksowej formie wielu funkcji określonej Fouriera

Charakterystyka widmowa rzędu

Wyrażenie W wielu wywołach n.Harmonijka.Wiadomo, że

gdzie lub.

,

Agregat, zwany odpowiednio spektrum amplitudy i fazyczasowisko.

Graficznie widma przedstawiono w postaci długości przeprowadzonej prostopadle do osi, na której stosuje się wartość n.= 1.2 ... lub.

Graficzny obraz Odpowiednie widmo nazywane jest diagramem amplitudy lub fazy. W praktyce najczęściej stosuje się widmo amplitudy.

. Przykład rozwiązywania problemów

Zadanie 2.: Rozważmy konkretny przykład Zadania dla wybranego modelu procesu fizycznego.

Będziemy kontynuować tę funkcję do całej osi numerycznej, otrzymujemy okresową funkcję fA.(x.) C przez okres t \u003d 2 l.\u003d 18 (Rys. 1.).

Figa. 1. Harmonogram Okresowo kontynuacja funkcji

Oblicz współczynniki Fouriera określonej funkcji.

Piszemy częściowe sumy serii:

Figa. 2. Częściowe kwoty Fouriera

Z wzrostem n. Częściowe wykresy podsumowujące w punktach ciągłości zbliżają się do grafiki funkcyjnej. fA.(x.) . W punktach przerwami zbliżają się wartości kwot częściowych .

Konstruujemy diagramy amplitudy i fazy.

Biorąc pod uwagę kwartał.

Stół

4. Przykładowy problem rozwiązywania problemów w środowisku Matlab R2009A

Zadanie 3: Jako przykład rozważ całe interwały PR i QT.

Figa

W tym funkcji buduj wykresy kwot częściowych, a także diagramów amplitudy i fazy.

Podejmij konkretne wartości parametrów do naszego zadania:

Skrypt do budowy wymaganych wykresów i wykresów.

Skrypt umożliwia rozwiązanie wielu podobnych zadań, wybierając parametry i współrzędne punktów Q, R, S.

% Obliczanie kwot częściowych i charakterystyki widmowej serii Fouriera do jawnego

% Analizy widmowej.L I1 I2 q R S I3 I4 I5 P T W V V A B C D P R qy qy Sy Nase \u003d 18; \u003d 6; I2 \u003d 10; Q \u003d 11; Qy \u003d -2; R \u003d 12; Ry \u003d 17; S \u003d 13; Sy \u003d -4; I3 \u003d 15; I4 \u003d 20; I5 \u003d 26; \u003d 2; T \u003d 3; Exprnum \u003d 9; \u003d 250; \u003d 30; \u003d 0; flaga \u003d\u003d 0 \u003d 1; (k<15)

k \u003d menu ("zmiana parametrów", ...

sprintF ("parametry1 p \u003d% g", p), ... ("parametry2 i1 \u003d% g", I1), ... ("Parameter3 i2 \u003d% g", I2), ... ("parametry4 qx \u003d% g ", q), ... (" parametry5 qy \u003d% g ", qy), ... (" Parametr 6 rx \u003d% g ", r), ... (" parametry7 Ry \u003d% G " , Ry), ... ("Parameter8 SX \u003d% G", S), ... ("Parametr 9 SY \u003d% G", SY), ... ("Parameter10 I3 \u003d% G", I3), ... ("Parameter11 i4 \u003d% G", I4), ... ("Parameter12 t \u003d% g", t), ... ("Parameter13 i5 \u003d% G", I5), ... (" Parameter13 NS \u003d% G, NS), ...

"Kontynuuj"); k \u003d\u003d 1, \u003d wejście ();

endek \u003d\u003d 2, \u003d wejście ();

endek \u003d\u003d 3, \u003d wejście ();

endek \u003d\u003d 4, \u003d wejście ();

endek \u003d\u003d 5, \u003d wejście ();

endek \u003d\u003d 6, \u003d wejście ();

endek \u003d\u003d 7, \u003d wejście ();

"Nowa wartość SX \u003d"]);

endek \u003d\u003d 9, \u003d wejście ();

endek \u003d\u003d 10, \u003d wejście ();

endek \u003d\u003d 11, \u003d wejście ();

endek \u003d\u003d 12, \u003d wejście ();

endek \u003d\u003d 13, \u003d wejście ()

endek \u003d\u003d 14, \u003d wejście ()

% Parametrów aplikacji \u003d QY / (Q-I2);

v \u003d QY * I2 / (I2-Q); \u003d (Ry-QY) / (RQ); \u003d (QY * RQ * RY) / (RQ); \u003d (SY-RY) / (SR); \u003d (Ry * SR * SY) / (SR); \u003d SY / (S-I3); \u003d I3 * SY / (I3-S); \u003d 2 * L / N; \u003d 0: TS: 2 * L; \u003d Długość (t ); \u003d Zer (1, Dim); \u003d podłoga (I1 * N / 2 / L) +1; \u003d podłoga ((I2-I1) * N / 2 / L) +1; \u003d podłoga ((Q-I2) * N / 2 / L) +1; \u003d podłoga (RQ) * N / 2 / L) +1; \u003d podłoga ((SR) * N / 2 / L) +1; \u003d podłoga ((I3-S) * N / 2 / L) +1; \u003d podłoga ((I4-I3) * N / 2 / L) +1; \u003d podłoga ((I5-I4) * N / 2 / L) +1; \u003d podłoga ((( 2 * L-I4) * N / 2 / L) +1; I \u003d 1: U1 (I) \u003d P * SIN (PI * T (I) / I1); I \u003d U1: U2 (I) \u003d 0; i \u003d (U2 + U1) :( U3 + U2 + U1) (I) \u003d W * T (I) + V; I \u003d (U3 + U2 + U1): (U4 + U3 + U2 + U1) (I) \u003d A * T (I) + B; I \u003d (U4 + U3 + U2 + U1): (U5 + U4 + U3 + U2 + U1) (I) \u003d C * T (I) + D; I \u003d (U5 + U4 + U3 + U2 + U1): (U6 + U5 + U4 + U3 + U2 + U1) (I) \u003d q * t (i) + r; i \u003d (U6 + U5 + U4 + U3 + U2 + U1 ): (U7 + U6 + U5 + U4 + U3 + U2 + U1) (I) \u003d 0; I \u003d (U7 + U6 + U5 + U4 + U3 + U2 + U1): (U8 + U7 + U6 + U5 + U4 + U3 + U2 + U1) (I) \u003d T * SIN (PI * (T (I) -I4) / (I5-I4)); (T, Y, "Linewidth", 2), siatka, zestaw ( GCA, "Fontname", "Arial Cyr", "Fontsyze", 16);

tytuł ("wykres procesowy"); Xlabel ("Czas (C)"); ylabel ("y (t)");

% Wykres częściowy

n \u003d 0; j \u003d 1: exprnum \u003d j; j1 \u003d quad (@f, 0, I1); 2 \u003d A0 + Quad (@f, I1, I2); 3 \u003d A0 + Quad (@f, I2, Q ); 4 \u003d A0 + quad (@f, q, r); 5 \u003d A0 + quad (@f, R, S); 6 \u003d A0 + Quad (@f, S, I3); 7 \u003d A0 + Quad ( @F, I3, I4); 8 \u003d A0 + Quad (@f, I4, I5); 9 \u003d A0 + Quad (@f, I5, 2 \u200b\u200b* L); \u003d A0 / L; \u003d Zer (1, NS) ; \u003d zer (1, ns); i \u003d 1: ns \u003d i; j \u003d 1: exprnum \u003d j; j1 (i) \u003d quad (@f, 0, i1); (i) \u003d quad (@ g, 0 , I1); 2 (i) \u003d (i) + quad (@f, i1, i2); (i) \u003d bn (i) + quad (@ g, i1, i2); 3 (i) \u003d an ( i) + quad (@f, i2, q); (i) \u003d bn (i) + quad (@ @g, i2, q); 4 (i) \u003d an (i) + quad (@f, q, r ); (i) \u003d bn (i) + quad (@ g, q, r); 5 (i) \u003d an (i) + quad (@f, r, s); (i) \u003d bn (i) + quad (@ g, r, s); 6 (i) \u003d an (i) + quad (@f, s, i3); (i) \u003d bn (i) + quad (@ g, s, i3); (i) \u003d (I) + quad (@f, I3, I4); (i) \u003d BN (I) + Quad (@ @g, I3, I4); 8 (i) \u003d AN (I) + Quad ( @f, I4, I5); (i) \u003d BN (I) + quad (@ μg, I4, I5); 9 (I) \u003d (i) + Quad (@f, I5, 2 \u200b\u200b* L) ( i) \u003d bn (i) + quad (@ g, i5, 2 * l); (i) \u003d (i) / l; (i) \u003d bn (i) / l; \u003d t; \u003d zer (1, Długość (x)); \u003d fn + a0 / 2; i \u003d 1: ns \u003d i; \u003d fn + an (i) * cos (n * pi * x / l) + bn (i) * sin (n * pi * X / L); (T, Y, X, FN, "Linewidth", 2), siatka, zestaw (GCA "Fontname", "Arial Cyr", "Fontsyze", 16);

tytuł ("sygnał i suma częściowa"); Xlabel ("Czas (C)"); Ylabel (Sprintf ("SN (T)"));

% Budowa diagramu amplitudy \u003d zer (1, NS);

wN \u003d PI / L; \u003d WN: WN: WN * NS; I \u003d 1: NS (I) \u003d SQRT (I). ^ 2 + BN (I). ^ 2); (GN, A, ". "), Siatka, zestaw (GCA," Fontname "," Arial Cyr "," Fontsyze ", 16); (diagram sygnału amplitudy"); Xlabel ("n"); ylabel ("an");

% Budowa diagramu fazowego sygnału \u003d zer (1, NS);

dla I \u003d 1: NS ((I)\u003e 0) (I) \u003d ATAN (BN (I) / A (I)); (I)<0)&&(bn(i))>0) (I) \u003d ATAN (BN (I) / A (I)) + PI; ((I)<0)&&(bn(i))<0)(i)=pi-atan(bn(i)/an(i));((an(i)==0)&&(bn(i))>0) (I) \u003d PI / 2; ((i) \u003d\u003d 0) && (bn (i))<0)(i)=-pi/2;(Gn,Fi,"."), grid, set(gca,"FontName","Arial Cyr","FontSize",16);("Фазовая диаграмма сигнала"); xlabel("n"); ylabel("Fi");Figure 1;Figure 2;Figure 3;Figure 4;=0;=input("Закончить работу-<3>, kontynuować - ");

Listaliteratura

1. Fichtenhalz, G.m. Kurs różnicowy i integralny: przy 3 t., M., 1997. 3 tony.

Wenev, V. T., Naumowicz, A. F., Naumovich, N. F., główne wzory matematyczne. Mińsk, 1998.

Harkevich, A.a, widma i analiza. Moskwa, 1958.

Lazarev, Yu. F., rozpocznij programowanie w środowisku Matlab. Kijów 2003.

Demidovich, bp. Zbiór zadań i ćwiczeń na analizie matematycznej, M., 1988.

Wśród różnorodnych systemów funkcji ortogonalnych, które mogą być wykorzystywane jako podstawy do reprezentowania sygnałów inżynierii radiowej, funkcje harmoniczne (sinusoidalne i cosinus i cosinus) zajmują wyjątkowe miejsce. Wartość sygnałów harmonicznych dla inżynierów radiowych wynika z wielu powodów.

W szczególności:

1. Sygnały harmoniczne są niezmienne w odniesieniu do transformacji przeprowadzanych przez stacjonarne liniowe obwody elektryczne. Jeśli taki łańcuch jest podekscytowany źródłem oscylacji harmonicznych, sygnał na wyjściu łańcucha pozostaje harmonicznie z taką samą częstotliwością, różniące się od sygnału wejściowego tylko amplitudy i początkową fazę.

2. Technika do generowania sygnałów harmonicznych jest stosunkowo prosty.

Jeśli jakiś sygnał jest reprezentowany jako suma oscylacji harmonicznych o różnych częstotliwościach, powiedzą - że wykonywana jest rozkład widma tego sygnału. Oddzielne składniki harmoniczne sygnału stanowią spektrum.

2.1. Sygnały okresowe i wiersze Fourier

Model matematyczny procesu powtarzającego się w czasie jest sygnałem okresowym z następującym obiektem:

Tutaj T jest okresem sygnału.

Zadaniem jest znalezienie widmowego rozkładu takiego sygnału.

Fourier rząd.

Ustawmy czas omawiany w Ch. Podstępną podstawą utworzoną przez funkcje harmoniczne z wieloma częstotliwościami;

Każda funkcja z tej podstawy spełnia stan częstotliwości (2.1). Dlatego, - wykonując ortogonalną rozkład sygnału na tej podstawie, tj. Współczynniki obliczeniowe

dostajemy rozkład widma

targi przy całej nieskończoności osi czasu.

Seria gatunków (2.4) nazywana jest w pobliżu Fouriera sygnału DanRgo. Wprowadzamy główną częstotliwość sekwencji tworzącej sygnał okresowy. Obliczanie współczynników rozkładu (2.3), napisz serię Fouriera dla sygnału okresowego

z współczynnikami

(2.6)

Tak więc w ogólnym przypadku sygnał okresowy zawiera stały stały składnik i nieskończony zestaw oscylacji harmonicznych, tzw. Harmoniczne z częstotliwościami do wielu głównej częstotliwości sekwencji.

Każda harmonija może być opisana przez jego amplitudę i początkową fazę, współczynniki serii Fouriera powinny być napisane jako

Podstawianie tych wyrażeń w (2.5), otrzymujemy kolejny, - równoważna forma serii Fouriera:

który jest czasami wygodniejszy.

Schemat widmowy sygnału okresowego.

Jest więc zwyczajowo zadzwonić do graficznego obrazu współczynników serii Fouriera dla określonego sygnału. Diagramy widmowe amplitudy i fazy rozróżniają (rys. 2.1).

Tutaj wzdłuż osi poziomej częstotliwości harmonicznych są przełożone na jakąś skalę, a ich amplitudy i początkowe fazy są prezentowane wzdłuż osi pionowej.

Figa. 2.1. Diagramy widmowe pewnego okresowego sygnału: A - amplituda; B - faza

Szczególnie zainteresowany diagramem amplitudowym, który pozwala ocenić procentową zawartość niektórych harmonicznych w widmie sygnału okresowego.

Badamy kilka konkretnych przykładów.

Przykład 2.1. Wiersz czteroczna sekwencja okresowa prostokątnych impulsów wideo ze znanymi parametrami nawet względem punktu t \u003d 0.

W inżynierii radiowej stosunek nazywany jest wellness sekwencji. Według formuł (2.6) znajdziemy

Ostateczna formuła serii Fouriera jest wygodnie napisana w formularzu

Na rys. 2.2 Przedstawiono wykresy amplitudy sekwencji w dwóch skrajnych przypadkach.

Ważne jest, aby pamiętać, że sekwencja krótkich impulsów, co rzadko ma bogatą kompozycję widmową.

Figa. 2.2. Spektrum amplitudy okresowej sekwencji rhryaturgicznych impulsów wideo: a - z dużym obowiązkiem; B - z niskim obowiązkiem

Przykład 2.2. Seria czterorzędowej sekwencji okresowych impulsów utworzonych przez sygnał harmoniczny gatunków ograniczony na poziomie (zakłada się, że).

Wprowadzamy specjalny parametr - kąt wycięcia określony z stosunku z miejsca, w którym

W korespondencji, wartość jest równa okresie trwania jednego impulsu, wyrażonego w środku kątowym:

Nagrywanie analityczne pulsu generowania sekwencji w rozważaniu ma formularz

Stały składnik sekwencji

Współczynnik amplitudy pierwszej harmonicznej

Podobnie oblicz amplitudy - elementy harmoniczne, gdy

Wyniki są zwykle rejestrowane w następujący sposób:

gdzie tak zwane funkcje Berg:

Wykresy niektórych funkcji Berg są pokazane na FIG. 2.3.

Figa. 2.3. Wykresy kilku pierwszych funkcji Berg

Złożona forma serii Fouriera.

Rozkład widmowy sygnału okresowego można wykonać przez kilka jonów przy użyciu systemu podstawowych funkcji składających się z wykładnika z wyimaginowanym wskaźnikiem:

Łatwo jest zobaczyć, że funkcje tego systemu są okresowe z okresem okontormalizacji od czasu

W tym przypadku zajmuje szereg Fourier z dowolnego sygnału okresowego

z współczynnikami

Zazwyczaj używaj następującej formy nagrywania:

Wyrażenie (2.11) to seria Fouriera w kompleksowej formie.

Spektrum sygnału zgodnie z wzorem (2.11) zawiera komponenty na ujemnej częstotliwości pół-jednej, i. W liczbie (2,11) składniki z pozytywnymi i negatywnymi częstotliwościami są łączone na pary, na przykład.

W wielu przypadkach zadanie uzyskania (obliczania) widma sygnalizacyjnego jest następujące. Istnieje ADC, który, z częstotliwością próbkowania FD, konwertuje ciągły sygnał nadchodzący do wejścia na czas T, do liczb cyfrowych - n kawałków. Następnie tablica próbki jest podawana do określonego programu, który daje dowolne numeryczne wartości liczbowe (programista Wyciągnięty z Ita Wysłany przez program, zapewnia, że \u200b\u200bwykonuje transformację Fouriera).

Aby sprawdzić, czy program działa poprawnie, tworzą tablicę próbek jako sumę dwóch sinusoidów grzechu (10 * 2 * PI * X) + 0,5 * SIN (5 * 2 * PI * X) i ssać program. Program wyciągnął następujące elementy:

harmonogram sygnału Rys.1

rys.2 Harmonogram widma sygnału

Wykres widma ma dwa patyki (harmoniczne) 5 Hz z amplitudy 0,5 V i 10 Hz - z amplitudy 1 V, wszystko jak w formule źródłowej. Wszystko jest w porządku, programista jest dobrze zrobiony! Program działa poprawnie.

Oznacza to, że jeśli dostarczymy prawdziwy sygnał z mieszaniny dwóch sinusoidów do wejścia ADC, będziemy uzyskać podobne widmo składające się z dwóch harmonicznych.

Całkowity, nasza real Zmierzony sygnał czas trwania 5 sekund, zdigitalizowany ADC, to jest reprezentowany oddzielny Referencje, ma dyskretny nieuzasadniona widmo.

Z matematycznego punktu widzenia - ile błędów w tej frazie?

Teraz szefowie zdecydowali, że zdecydowaliśmy, że 5 sekund jest zbyt długi, miejmy pomiar sygnału przez 0,5 sekundy.



rys.3 Funkcja SIN (10 * 2 * PI * X) + 0,5 * SIN (5 * 2 * PI * X) W okresie pomiarowym 0,5 sekundy

funkcja FIG.4 Spectrum.

Coś takiego nie! Harmonica 10 Hz jest zwykle rysowane, a zamiast kij na 5 Hz pojawił się kilka niezrozumiałe harmonikę. Patrzymy w Internet, co tak ...

W, mówią, że na końcu próbki konieczne jest dodanie zera i spektrum zostaną narysowane normalnie.

rys.5 wykończone zer do 5 sekund

rys.6 otrzymała widmo

W każdym razie, a nie co było 5 sekund. Będziemy musieli poradzić sobie z teorią. Idziemy B. Wikipedia. - źródło wiedzy.

2. Ciągła funkcja i prezentowanie go w pobliżu Fouriera

Matematycznie, nasz czas trwania sygnału T Secox jest funkcją F (x) określoną w segmencie (0, T) (X w tym przypadku - czas). Taka funkcja może być zawsze reprezentowana jako suma funkcji harmonicznych (sinusoidalna lub cosinus) formularza:

(1), gdzie:

K - liczba funkcji trygonometrycznej (liczba składników harmonicznych, numer harmoniczny)
T - Segment, w którym zdefiniowana jest funkcja (czas trwania sygnału)
AK - Amplituda komponentu harmonicznego K-TH,
k- początkowa faza składnika harmonicznego K-TH

Co to znaczy "przedstawić funkcję w formie sumy serii"? Oznacza to, że składając w każdym punkcie wartość komponentów harmonicznych serii Fouriera, otrzymujemy wartość naszej funkcji w tym momencie.

(Bardziej poważne odchylenie kwadratowe wiersza z funkcji F (X) będzie dążyć do zera, ale pomimo konwergencji RMS, seria Fouriera funkcji, ogólnie rzecz biorąc, nie jest zobowiązana do zbiegania się do niego. Patrz HTTPS: / /ru.wikipedia.org/ Wiki / Russian_Fourier.)

Ta seria może być również rejestrowana w formularzu:

(2),
Gdzie k-i skomplikowana amplituda.

Związek między współczynnikami (1) a (3) wyraża następujące wzory:

Należy pamiętać, że wszystkie te trzy reprezentacje serii Fouriera są całkowicie równoważne. Czasami podczas pracy z wierszami Fourier, wynagrodzenie jest wygodniejsze w użyciu wykładników wyimaginowanego argumentu zamiast zatoków i cosinus, czyli, aby stosować transformację Fouriera w kompleksowej formie. Ale jest to wygodne dla nas użycie wzoru (1), gdzie seria Fouriera jest reprezentowana jako cosinus kanał z odpowiednimi amplitudami i fazami. W każdym razie jest nieprawidłowy, że wynik transformacji fouriera rzeczywistego sygnału będzie złożone amplitudy harmonicznych. Jak mówi w Wiki "Transformacja Fouriera (ℱ) - operacja, która porównuje jedną funkcję innej funkcji zmiennej rzeczywistej, również rzeczywistą zmienną".

CAŁKOWITY:
Podstawą matematyki analizy widmowej sygnałów jest transformacja Fouriera.

Transformacja Fouriera umożliwia reprezentowanie funkcji ciągłej F (X) (sygnał), zdefiniowany w segmencie (0, T) jako sumę nieskończonej liczby (nieskończony wiersz) funkcji trygonometrycznych (sinusoid i cosinus) z pewnymi amplitudami i fazy, również rozważane w segmencie (0, t). Taka liczba jest nazywana w pobliżu Fouriera.

Zauważamy kilka punktów, których zrozumienie jest wymagane, aby prawidłowo korzystać z transformacji Fouriera do analizy sygnałów. Jeśli rozważymy zakres Fouriera (suma sinusoidy) w całej osi X, możesz zobaczyć, że poza segmentem (0, t) funkcja prezentowana obok Fouriera będzie okresowo powtarzać naszą funkcję.

Na przykład na rys.7 Wykres, czynność początkową jest zdefiniowana w segmencie (-T 2, + T 2), a zakres Fouriera reprezentuje okresową funkcję zdefiniowaną na całej osi X.

Dzieje się tak dlatego, że sami sinusoidy są odpowiednio okresowymi funkcjami, ich suma będzie okresową funkcją.

rys.7 Reprezentacja funkcji źródła nieredotykowego w pobliżu Fouriera

W ten sposób:

Nasza funkcja początkowej jest ciągła, nieuzasadniona, określona na określonej długości T.
Spektrum tej funkcji jest dyskretne, czyli, jest on przedstawiony w postaci nieskończonej gamy komponentów harmonicznych - serii Fouriera.
W rzeczywistości blisko Fouriera określa pewną funkcję okresową, która zbiega się z naszymi w segmencie (0, T), ale dla nas to okresowość nie jest znacząca.

Okresy składników harmonicznych są wielokrotnością rozmiaru segmentu (0, T), który określa funkcję początkową F (X). Innymi słowy, okresy harmoniczne mają wiele czasu trwania pomiaru sygnału. Na przykład pierwszy okres harmoniczny serii Fouriera jest równy interwałowi, który określa funkcję F (X). Okres drugiej harmonicznej serii Fouriera jest równa interwałowi T / 2. I tak dalej (patrz rys. 8).

rys.8 Okresy (częstotliwości) składników harmonicznych serii Fourier (tutaj t \u003d 2π)

W związku z tym częstotliwości składników harmonicznych wartości wielu wartości 1 / t. Oznacza to, że częstotliwości składników harmonicznych FK są równe FK \u003d K., gdzie wartości od 0 do ∞, na przykład, do \u003d 0 F0 \u003d 0; k \u003d 1 f1 \u003d 1 k \u003d 2 F2 \u003d 2 K \u003d 3 F3 \u003d 3 \\ t; ... FK \u003d K (w zerowej częstotliwości - składnik stałego).

Pozwól naszej funkcji początkowej, reprezentują sygnał nagrany podczas t \u003d 1 sek. Następnie pierwszy okres harmoniczny będzie równy czas trwania naszego sygnału T1 \u003d T \u003d 1 sekund, a częstotliwość harmoniczna wynosi 1 Hz. Okres drugiej harmonicznej będzie równe okresie trwania sygnału podzielonego przez 2 (T2 \u003d T / 2 \u003d 0,5 sekundy), a częstotliwość wynosi 2 Hz. Dla trzecich harmonicznych T3 \u003d T / 3 sekundy, a częstotliwość wynosi 3 Hz. Itp.

Krok między harmonikami w tym przypadku wynosi 1 Hz.

Zatem czas trwania sygnału 1 sekundy można rozłożyć na komponentach harmonicznych (uzyskać widmo) z rozdzielczością 1 Hz.
Aby zwiększyć rozdzielczość 2 razy do 0,5 Hz - konieczne jest zwiększenie czasu trwania pomiaru 2 razy do 2 sekund. Sygnał z czasem trwania 10 sekund można rozkładać na elementy harmoniczne (uzyskać widmo) o rozdzielczości częstotliwości 0,1 Hz. Nie ma innej rozdzielczości częstotliwości innych sposobów zwiększenia rozdzielczości.

Istnieje metoda sztucznego wzrostu czasu trwania sygnału, dodając zer do tablicy liczenia. Ale nie zwiększa rzeczywistej rozdzielczości częstotliwości.

3. Dyskretne sygnały i dyskretna transformacja Fouriera

Wraz z rozwojem technologii cyfrowej metody przechowywania danych pomiarowych (sygnały) zostały zmienione. Jeśli wcześniej sygnał może być zapisany na magnetofonie i zapisywany na taśmie w formie analogowej, teraz sygnały są zdigitalizowane i przechowywane w plikach w pamięci komputera jako zestaw liczb (próbek).

Zwykły diagram pomiaru i digitalizacji sygnału jest następujący.

fIG.9 Schemat kanałów pomiarowych

Sygnał z przetwornika pomiarowego przychodzi do ADC w okresie T. Otrzymany w czasie ton sygnału (próbki) są przesyłane do komputera i są przechowywane w pamięci.

rys.10 Digitized Signal - N Próbki odebrane podczas T

Jakie są wymagania przedstawione do parametrów cyfryzacji sygnału? Urządzenie przekształcające sygnał analogowy wejściowy do dyskretnego kodu (sygnał cyfrowy) nazywa się konwertera analogowo-cyfrowego (ADC, angielski. Analog-do cyfrowy konwerter, ADC) (Wiki).

Jednym z głównych parametrów ADC jest maksymalna częstotliwość pobierania próbek (lub częstotliwości sesji, angielski. Szybkość próbki) jest częstotliwość liczenia zliczania sygnału ciągła w czasie, gdy go dyskretuje. Mierzone w Hertz. ((Wiki))

Według twierdzenia Kotelnikowa, jeśli ciągły sygnał ma widmo, ograniczona częstotliwość FMAX, może być całkowicie i jednoznacznie przywrócona przez jego dyskretne odniesienia, podjęte w odstępach czasu . Dzięki częstotliwości FD ≥ 2 * Fmax, gdzie FD jest częstotliwością próbkowania; Fmax jest maksymalną częstotliwością widma sygnału. Innymi słowy, częstotliwość digitalizacji sygnału (częstotliwość dyskretyzacji ADC) powinna co najmniej 2 razy przekraczać maksymalną częstotliwość sygnału, który chcemy zmierzyć.

A co się wydarzy, jeśli bierzemy liczy się mniejszą częstotliwością niż wymagana przez twierdzenie Kotelnikowa?

W tym przypadku występuje efekt "aliasingu" (jest to efekt stroboskopowy, efekt molowy), w którym sygnał wysokiej częstotliwości po digitalizacji zamienia się w sygnał niskiego częstotliwości, który w rzeczywistości nie istnieje. Na rys. 11 Sinusoid czerwonej częstotliwości jest prawdziwym sygnałem. Niebieski sinusoid o niższej częstotliwości jest fikcyjnym sygnałem, który występuje z powodu czasu podjęcia czasu referencyjnego, aby przejść ponad pół okresu sygnału o wysokiej częstotliwości.

Figa. 11. Wygląd fałszywego sygnału niskiego częstotliwości z niewystarczającą częstotliwością próbkowania

Aby uniknąć wpływu aliasingu, zanim ADCS umieściły specjalny filtr antyaliasowy - FNH (dolny filtr częstotliwości), który przekazuje częstotliwość poniżej połowy częstotliwości dyskretyzacji ADC oraz wyższych akcji częstotliwości.

Aby obliczyć spektrum sygnału na dyskretnych odniesień, stosuje się dyskretną transformację Fouriera (DFT). Uwaga Po raz kolejny, że spektrum sygnału dyskretnego "z definicji" jest ograniczony przez częstotliwość FMAX, mniej niż połowę częstotliwości próbkowania FD. Dlatego spektrum sygnału dyskretnego może być reprezentowany przez ilość ostatniej liczby harmonicznych, w przeciwieństwie do nieskończonej ilości dla serii sygnału ciągłego Fouriera, którego widmo mogą być nieograniczone. Zgodnie z twierdzeniem Kotelnikowa maksymalna częstotliwość harmoniczna powinna być taka, że \u200b\u200bco najmniej dwa liczenia stanowiły co najmniej, dlatego liczba harmonicznych jest połową liczby próbek sygnału dyskretnego. Oznacza to, że jeśli w próbce znajdują się N, liczba harmonicznych w widmie będzie n / 2.

Rozważ teraz dyskretną transformację Fouriera (DFT).

W porównaniu z Fourier

Widzimy, że pokrywają się, z wyjątkiem tego, że czas w DFT ma dyskretną naturę, a liczba harmonicznych jest ograniczona przez N / 2 - połowa liczników.

Wzory DAK są rejestrowane w zmiennych liczb całkowitych bezwymiarowych K, S, gdzie K jest liczbą numerów próbek sygnału, S - liczba komponentów widmowych.
Wartość S przedstawia liczbę pełnych oscylacji harmonicznych w okresie t (czas trwania pomiaru sygnału). Dyskretna transformacja Fouriera jest używana do znalezienia amplitudów i faz harmonicznych metodą numeryczną, tj. "na komputerze"

Wracając do uzyskanych wyników na początku. Jak wspomniano powyżej, podczas rozkładania Fouriera funkcji nieredotykowej (naszego sygnału), wynikowa seria Fouriera faktycznie odpowiada okresowej funkcji z okresem T. (Fig. 12).

rys.12 Funkcja okresowa F (X) z okresem T0, z okresem pomiarowym T\u003e T0

Jak widać na rys.12, funkcja F (X) jest okresowa z okresem T0. Jednak ze względu na to, że czas trwania próbki pomiarowej T nie pokrywa się z okresem funkcji T0, funkcja uzyskana jako seria Fouriera ma przerwę w punkcie T. W rezultacie spektrum tej funkcji będzie zawierać dużą liczbę harmonicznych wysokiej częstotliwości. Jeśli czas trwania próbki pomiarowej T Zbiegł się z okresem funkcji T0, tylko pierwsze harmoniczne (sinusoid z okresem równym okresie trwania próbki) byłoby obecne w widmie uzyskanym po transformacji Fouriera), ponieważ F (x) Funkcja jest sinusoidem.

Innymi słowy, program DPT "nie wie", że nasz sygnał reprezentuje "kawałek sinusoidów" i próbuje przedstawić okresową funkcję w postaci liczby, która ma szczelinę z powodu nie pociągnięcia poszczególnych plastrów sinusoidów .

W rezultacie harmoniczne pojawiają się w widmie, które powinny w ilości przedstawienia formy funkcji, w tym tej luki.

Zatem, aby uzyskać "prawidłowe" spektrum sygnału, który jest sumą kilku sinusoidów o różnych okresach, konieczne jest, aby cała liczba każdego okresów sinusoidalnych została złożona w okresie pomiaru sygnału. W praktyce warunek ten można wykonać z wystarczająco dużym czasem pomiaru sygnału.

Rys.13 Przykładowa funkcja i spektrum błędu kinematycznego skrzyni biegów

W mniejszym czasie, obraz będzie wyglądał gorszy:

Rys.14 Przykładowa funkcja i spektrum sygnału wibracyjnego wirnika

W praktyce trudno jest zrozumieć, gdzie "prawdziwe składniki" i gdzie "artefakty" spowodowane przez rosnące okresy składników i czas trwania próbki sygnału lub "skacze i pęknie" formularza sygnału. Oczywiście słowa "prawdziwe komponenty" i "artefakty" nie są na próżno w cytatach. Obecność na harmonogramie widma zestawu harmonicznego nie oznacza, że \u200b\u200bnasz sygnał w ich rzeczywistości "składa się". Nie obchodzi to, że numer 7 "składa się z liczb 3 i 4. Numer 7 może być reprezentowany jako suma liczb 3 i 4 - jest poprawna.

Więc nasz sygnał ... i raczej, nawet "nasz sygnał", a funkcja okresowa, skomponowana przez powtórzenie naszego sygnału (próbki), może być reprezentowany jako suma harmonicznych (sinusoid) z pewnymi amplitudami i fazami. Ale w wielu ważnych przypadkach (patrz rysunki powyżej), jest rzeczywiście możliwe, aby skojarzyć harmoniczne uzyskane w widmie oraz z realnymi procesami, które mają charakter cykliczny i przyczyniając się do znacznego wkładu w formularz sygnalizacyjny.

Niektóre wyniki.

1. Prawdziwy zmierzony sygnał, czas trwania t S, cyfrowy ADC, który jest przedstawiony z zestawem dyskretnych próbek (N Sztuce), ma dyskretny spektrum nieuzasadnione reprezentowane przez zestaw harmonicznych (N / 2 sztuk).

2. Sygnał jest reprezentowany przez zestaw ważnych wartości, a jego widmo jest reprezentowane przez zestaw prawidłowych wartości. Częstotliwości harmoniczne są pozytywne. Fakt, że matematyka jest wygodniejsza do przedstawienia widma w kompleksowej formie przy użyciu negatywnych częstotliwości, nie oznacza, że \u200b\u200b"tak prawidłowo" i ", więc zawsze musi zrobić".

3. Sygnał mierzony w segmencie Time T jest zdefiniowany tylko na długości czasu, w którym było przed rozpoczęciem pomiaru sygnału, a co się wydarzy po tym, jak nauka jest nieznana. W naszym przypadku nie jest interesujący. D PHT of time-limitation sygnał daje mu "prawdziwe" spektrum, w tym sensie, że w pewnych warunkach pozwala obliczyć amplitudę i częstotliwość swoich składników.

Używane materiały i inne użyteczne materiały.