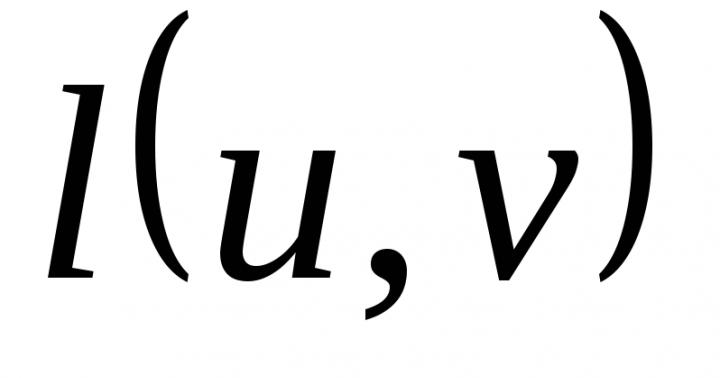Метод Дейкстри знаходження найкоротшого шляху. Графи. Знаходження найкоротшого відстані між двома вершинами за допомогою алгоритму Дейкстри. Схема реалізації послідовного алгоритму

Алгоритм Дейкстри - алгоритм на графах, який знаходить найкоротший шлях між двома даними вершинами в графі з невід'ємними довжинами дуг. Також часто ставиться завдання розрахунку найкоротшого шляху від даної вершини до всіх інших. Алгоритм широко застосовується в програмуванні, наприклад, його використовують протоколи маршрутизації.

опис

На вхід алгоритму подається зважений орієнтований граф з дугами неотрицательного ваги. На виході виходить набір найкоротших шляхів від даної вершини до інших.

На початку відстань для початкової вершини потрібно було рівним нулю, а відстані до всіх інших розуміються нескінченними. Масив прапорів, що позначають те, чи пройдена вершина, заповнюється нулями. Потім на кожному кроці циклу шукається вершина з мінімальним відстанню до початкової і прапором рівним нулю. Для неї встановлюється прапор і перевіряються всі сусідні вершини. Якщо розраховане раніше відстань від вихідної вершини до перевіряється більше, ніж сума відстані до поточної вершини і довжини ребра від неї до перевіряється вершини, то відстань до об'єкта аудиту вершини прирівнюємо до відстані до поточної + ребро від поточної до перевіряється. Цикл завершується, коли прапори всіх вершин стають рівні 1, або коли відстань до всіх вершин c прапором 0 нескінченно. Останній випадок можливий тоді і тільки тоді, коли граф несвязений.

алгоритм Дейкстри в псевдокоді

Вхід: З : Array of real - матриця довжин дуг графа; s - вершина, від якої шукається найкоротший шлях і t - вершина, до якої він шукається.

Вихід: вектори Т: array of real; і Н: array of 0..р. якщо вершина v лежить на найкоротшому шляху від s до t, то T [v]- довжина найкоротшого шляху від s до у; Н [у] - вершина, безпосередньо передує у на найкоротшому шляху.

Н - масив, в якому вершині n відповідає вершина m, попередня на шляху до n від s.

T - масив, в якому вершині n відповідає відстань від неї до s.

X - масив, в якому вершині n відповідає 1, якщо шлях до неї відомий, і 0, якщо немає.

ініціалізація масивів:

for v from 1 to р do

Т [v]: = ∞ (Найкоротший шлях невідомий)

X [v]: \u003d 0 (всі вершини не зазначені)

H [s]: \u003d 0 ( s нічого не передує)

T [s]: \u003d 0 (найкоротший шлях має довжину 0 ...)

X [s]: \u003d 1 (... і він відомий) v : = s (Поточна вершина)

М: (Оновлення позначок)

for і ∈ Г ( і) do

if Х [і] = 0 & Т [і]> T [v] + C then

Т [і]: = T [v] + C (Знайдений коротший шлях з s в і через v }

H [u]:= v (Запам'ятовуємо його)

m: = ∞

v : = 0

(Пошук кінця найкоротшого шляху)

for і from 1 to p do

if X [u] = 0 & T [u]< t then

v:= u;

m:= T [u] (вершина v закінчує найкоротший шлях з s

if v = 0 then

stop (немає шляху з s в t) End if

if v= t then

stop (знайдений найкоротший шлях з s в t) End if

X [v]: \u003d 1 (знайдено найкоротший шлях з s в v ) goto M

обгрунтування

Для доказу коректності алгоритму Дейкстри досить помітити, що при кожному виконанні тіла циклу, який починається міткою М, як vвикористовується вершина, для якої відомий найкоротший шлях з вершини s.Іншими словами, якщо X [v] \u003d 1, то T [v] \u003d d (s, v) , і все вершини на шляху (s, v), що визначається вектором Н, володіють тим же властивістю, тобто

Vu Т [і] \u003d 1 \u003d\u003e Т [і] \u003d d (s, u) & T] \u003d 1.

Дійсно (по індукції), перший раз в якості v використовується вершина s, для якої найкоротший шлях порожньої і має довжину 0 (непусті шляху не можуть бути коротшими, бо довжини дуг невід'ємні). Нехай Т [u] \u003d d (s, u) для всіх раніше помічених вершин і. Розглянемо знову позначену вершину v, Яка обрана з умови T [v] \u003d min Т [і]. Зауважимо, що якщо відомий шлях, що проходить через помічені вершини, то тим самим відомий найкоротший шлях. Припустимо (від противного), що T [v]\u003e d (s, v), тобто знайдений шлях, що веде з sв v,не є найкоротшим. Тоді на цьому шляху повинні бути непомічені вершини. Розглянемо першу вершину wна цьому шляху, таку що T [w] = 0.Імеем: T [w] = d (s, w) ⩽d (s\u003e v)< Т[v],что противоречит выбору вершины u.

тимчасова складність

Складність алгоритму Дейкстри залежить від способу місцезнаходженням не відвіданих вершини з мінімальним відстанню до початкової, способу зберігання безлічі невідвіданих вершин і способи оновлення міток. Нехай n кількість вершин, а через m - кількість ребер в графі. Тоді в найпростішому випадку, коли для пошуку вершини з мінімальним відстанню до початкової вершини проглядається все безліч вершин, а для зберігання відстаней використовується масив, час роботи алгоритму - О (n 2). Основний цикл виконується порядку n раз, в кожному з них на знаходження мінімуму витрачається близько n операцій. На цикли по сусідах кожної відвідуваною вершини витрачається кількість операцій, пропорційне кількості ребер m (оскільки кожне ребро зустрічається в цих циклах рівно двічі і вимагає константне число операцій). Таким чином, загальний час роботи алгоритму O (n 2 + m), але, так як m багато менше n (n-1), в кінцевому рахунку виходить О (n 2).

Для розріджених графів (тобто таких, для яких m багато менше n²) невідвіданих вершини можна зберігати в двійковій купі, а в якості ключа використовувати значення відстаней. Так як цикл виконується порядку n раз, а кількість релаксації (змін міток) не більш m, час роботи такої реалізації - О (nlogn + mlogn)

приклад

Обчислення відстаней від вершини 1 по прохідним вершин:

До кожного міста області (якщо рухатися можна тільки по дорогах).

Варіант 2. Є деяка кількість авіарейсів між містами світу, для кожного відома вартість. Вартість перельоту з A в B може бути не дорівнює вартості перельоту з B в A. Знайти маршрут мінімальної вартості (можливо, з пересадками) від Копенгагена до Барнаула.

формальне визначення

приклад

Розглянемо виконання алгоритму на прикладі графа, показаного на малюнку.

Нехай потрібно знайти найкоротший відстані від 1-ї вершини до всіх інших.

Реалізації на мовах програмування

Виконання в мові С (Сі)

#define SIZE 6 #define INF 1000000000 int a [SIZE] [SIZE] \u003d ((INF, 5, INF, INF, INF, INF), (1, 2, 3, 4, 5, 6), // матриця шляхів (1, 2, 3, 4, 5, 6), (1, 2, 3, 4, 5, 6), // індекси по горизонталі з точки { 1 , 2 , 3 , 4 , 5 , 6 },{ 1 , 2 , 3 , 4 , 5 , 6 }}; // по вертикалі в точку, значення - вага int d [SIZE]; // масив знайдених найкоротших шляхів, індекси - вершини графа void deikstra () (int v [SIZE]; // масив міток int temp, i; int minindex, min; for (i \u003d 0; i< SIZE ; i ++ ) { d [ i ] = INF ; // масив шляхів инициализируется нескінченністю v [i] \u003d 1; ) D [0] \u003d 0; do ( // виконання алгоритму minindex \u003d INF; min \u003d INF; for (i \u003d 0; i< SIZE ; i ++ ) { if ((v [ i ] == 1 ) && (d [ i ] < min )) { min = d [ i ]; minindex = i ; } } if (minindex != INF ) { for (i = 0 ; i < SIZE ; i ++ ) { if (a [ minindex ][ i ] > 0) (temp \u003d min + a [minindex] [i]; if (temp< d [ i ]) d [ i ] = temp ; } } v [ minindex ] = 0 ; } } while (minindex < INF ); }

найкоротшого шляху на сьогоднішній день є життєво необхідним завданням і використовується практично скрізь, починаючи від перебування оптимального маршруту між двома об'єктами на місцевості (наприклад, найкоротший шлях від будинку до університету), в системах автопілота, для знаходження оптимального маршруту при перевезеннях, комутації інформаційного пакету в мережах і т.п.

Найкоротший шлях розглядається за допомогою деякого математичного об'єкта, званого графом. Пошук найкоротшого шляху ведеться між двома заданими вершинами в графі. Результатом є шлях, тобто послідовність вершин і ребер, інцидентних двом сусіднім вершинам, і його довжина.

Розглянемо три найбільш ефективних алгоритму знаходження найкоротшого шляху:

• алгоритм Дейкстри;
• алгоритм Флойда;
• переборні алгоритми.

Зазначені алгоритми легко виконуються при малій кількості вершин у графі. При збільшенні їх кількості завдання пошуку найкоротшого шляху ускладнюється.

алгоритм Дейкстри

Даний алгоритм є алгоритмом на графах, який винайдений нідерландським вченим Е. Дейкстрой в 1959 році. Алгоритм знаходить найкоротша відстань від однієї з вершин графа до всіх інших і працює тільки для графів без ребер негативного ваги.

Кожній вершині приписується вага - це вага шляху від початкової вершини до даної. Також кожна вершина може бути виділена. Якщо вершина виділена, то шлях від неї до початкової вершини найкоротший, якщо немає - то тимчасовий. Обходячи граф, алгоритм вважає для кожної вершини маршрут, і, якщо він виявляється найкоротшим, виділяє вершину. Вагою даної вершини стає вага шляху. Для всіх сусідів даної вершини алгоритм також розраховує вага, при цьому ні за яких умов не виділяючи їх. Алгоритм закінчує свою роботу, дійшовши до кінцевої вершини, і вагою найкоротшого шляху стає вага кінцевої вершини.

алгоритм Дейкстри

Крок 1. Всім вершин, за винятком першої, присвоюється вага рівний нескінченності, а першій вершині - 0.

Крок 2. Всі вершини не виділено.

Крок 3. Перша вершина оголошується поточної.

Крок 4. Вага всіх невиділених вершин перераховується по формулі: вага невиділеної вершини є мінімальне число з старого ваги даної вершини, суми ваги поточної вершини і ваги ребра, що з'єднує поточну вершину з невиділеної.

Крок 5. Серед невиділених вершин шукається вершина з мінімальною вагою. Якщо така не знайдена, тобто вага всіх вершин дорівнює нескінченності, то маршрут не існує. Отже, вихід. Інакше, поточної стає знайдена вершина. Вона ж виділяється.

Крок 6. Якщо поточної вершиною виявляється кінцева, то шлях знайдений, і його вага є вага кінцевої вершини.

Крок 7. Перехід на крок 4.

У програмній реалізації алгоритму Дейкстри побудуємо безліч S вершин, для яких найкоротші шляхи від початкової вершини вже відомі. На кожному кроці до множини S додається та з решти вершин, відстань до якої від початкової вершини менше, ніж для інших, що залишилися вершин. При цьому будемо використовувати масив D, в який записуються довжини найкоротших шляхів для кожної вершини. Коли безліч S буде містити всі вершини графа, тоді масив D міститиме довжини найкоротших шляхів від початкової вершини до кожної вершині.

Крім зазначених масивів будемо використовувати матрицю довжин C, де елемент C - довжина ребра (i, j), якщо ребра немає, то її довжина покладається рівною нескінченності, тобто більше будь-якої фактичної довжини ребер. Фактично матриця C являє собою матрицю суміжності, В якій всі нульові елементи замінені на нескінченність.

Для визначення самого

5.4.3. Задача про найкоротший шлях і алгоритм Дейкстри її рішення

Нехай заданий орграф G(V, E), Кожній дузі якого поставлено у відповідність число
, зване довжиною дуги.

Визначення. довжиною шляху називається сума довжин дуг, що складають цей шлях. Задача про найкоротший шляхставиться так.

Варіант 1. Знайти довжини найкоротших шляхів (шляхів мінімальної довжини) і самі шляхи від фіксованої вершини s до всіх інших вершин графа.

Варіант 2. Знайти довжини найкоротших шляхів і самі шляхи між усіма парами вершин даного графа.

Якщо в графі є дуги негативною довжини, завдання може не мати рішень (втратить сенс). Це відбувається через те, що в графі може бути присутнім контур негативною довжини. Наявність контурів негативною довжини означає, що довжину шляху можна зробити рівний
. А якщо контурів негативною довжини немає, то найкоротші шляхи існують і будь-який найкоротший шлях - це проста ланцюг.

Зауважимо, що якщо найкоротший шлях існує, то будь-який його подпуть - це теж найкоротший шлях між відповідними вершинами.

Алгоритм Дейкстри рішення задачі про найкоротший шлях.

Алгоритм працює з дугами позитивної довжини і визначає найкоротші шляхи від фіксованої вершини s до всіх інших вершин графа. Позначимо ці вершини v 1 , v 2 ,…, v n .

Визначення. назвемо вершину u лежить ближче до вершини s, Ніж вершина v, Якщо довжина найкоротшого шляху від s до u менше довжини найкоротшого шляху від s до v. Будемо говорити, що вершини u і v рівновіддалені від вершини s, Якщо довжини найкоротших шляхів від s до u і от s до v збігаються.

Алгоритм Дейкстри послідовно впорядковує вершини графа в сенсі близькості до вершини s і заснований на наступних базових принципах.

Якщо довжини дуг - позитивні числа, то

найближча до s вершина - вона сама. Довжина найкоротшого шляху від s до s дорівнює 0;

найближча до s вершина, відмінна від s, Лежить від s на відстані однієї дуги  найкоротшою з усіх дуг, що виходять з вершини s;

будь-яка проміжна вершина найкоротшого шляху від s до деякої вершини v лежить ближче до s, Ніж кінцева вершина v;

найкоротший шлях до чергової впорядкованої вершини може проходити тільки через вже впорядковані вершини.

Нехай алгоритм вже упорядкував вершини v 1 , v 2 … v k . позначимо через
,
довжину найкоротшого шляху до вершини v i .

Розглянемо всі дуги вихідного графа, які починаються в одній з вершин безлічі
і закінчуються в ще невпорядкованих вершинах. Для кожної такої дуги, наприклад
, Обчислимо суму
. Ця сума дорівнює довжині шляху з s в y, В якому вершина v i є передостання вершина, а шлях з s в v i - найкоротший з усіх шляхів, що з'єднують s і v i .

Цим самим визначені довжини всіх шляхів з s в ще не впорядковані вершини, в яких проміжними вершинами є тільки вершини з числа k найближчих до s. Нехай найкоротший з цих шляхів закінчується на вершині w. тоді w і є
по близькості до s вершина.

Технічно дії за алгоритмом Дейкстри здійснюються за допомогою апарату відміток. мітка вершини v позначається як
. Будь-яка мітка - це число, що дорівнює довжині деякого шляху від s до v. Мітки діляться на тимчасові і постійні. На кожному кроці тільки одна мітка ставати постійною. Це означає, що її значення дорівнює довжині найкоротшого шляху до відповідної вершини, а сама ця вершина упорядковується. Номер черговий впорядкованої вершини позначимо літерою р.

опис алгоритму.

Крок 1. (Початкова установка). покласти
і вважати цю мітку постійною. покласти
,
і вважати ці мітки тимчасовими. покласти
.

Крок 2. (Загальний крок). він повторюється n раз, поки не будуть впорядковані всі вершини графа.

Перерахувати тимчасову мітку
всякої невпорядкованою вершини v i , В яку входить дуга, яка виходить з вершини р, за правилом

Вибрати вершину з мінімальною часовою міткою. Якщо таких вершин кілька, вибрати будь-яку.

нехай w- вершина з мінімальною часовою міткою. вважати мітку
постійної і покласти
.

Кроки алгоритму Дейкстри зручно оформляти в таблиці, кожен стовпець якої відповідає вершині графа. Рядки таблиці відповідають повторення загального кроку.

приклад. Для графа на рис. 4. Визначити найкоротші шляхи від вершин
до всіх інших вершин графа. Ребра означають дві різноспрямовані дуги однакової довжини.

Рішення. У табл. 1 записані мітки вершин на кожному кроці. Постійні мітки позначені знаком «+». Детально опишемо, як обчислюються мітки вершин.

З вершини 1 виходять дуги в вершини 2, 5, 6. Перераховуємо мітки цих вершин і заповнимо другий рядок таблиці.

Мітка вершини 6 ставати постійної,
.

З вершини 6 виходять дуги в ще невпорядковані вершини 2, 5, 8, 9. Перераховуємо їх тимчасові мітки

Заповнюємо 3 рядок таблиці. Мінімальна з тимчасових міток дорівнює 3 (мітка вершини 9),
.

З вершини 9 виходять дуги в ще невпорядковані вершини 5, 8, 11, 12. Тоді

Заповнюємо четвертий рядок таблиці. У цьому рядку дві вершини  2 і 12 мають мінімальні тимчасові мітки, рівні 4. Спочатку впорядкуємо, наприклад, вершину 2. Тоді на наступному кроці буде впорядкована вершина 12.

Таблиця 1

Отже,
.

З вершини 2 виходять дуги в ще невпорядковані вершини 3, 4, 5. Перераховуємо тимчасові мітки цих вершин

Заповнюємо 5 рядок таблиці. Мінімальна з тимчасових міток дорівнює 4 (мітка вершини 12),
.

Заповнюємо 6 рядок таблиці. Мінімальна з тимчасових міток дорівнює 5 (мітка вершини 5),
.

Заповнюємо 7 рядок таблиці. Ставати постійної мітка вершини 8 (вона дорівнює 5),
.

Вершина 11 упорядковується.

З вершини 11 виходять дуги в невпорядковані вершини 7, 10. Перераховуємо тимчасові мітки цих вершин

Вершина 4 отримує постійну мітку.

З вершини 4 виходять дуги в невпорядковані вершини 3, 7. Перераховуємо тимчасові мітки

Упорядковуємо вершину 3.

Заповнюємо 12 рядок таблиці. На цьому кроці упорядковуємо останню неупорядковану вершину 10.

Побудова дерева найкоротших шляхів.

Дерево найкоротших шляхів - це орієнтоване дерево з коренем у вершині S . Всі шляхи в цьому дереві - найкоротші для даного графа.

Дерево найкоротших шляхів будується по таблиці, в нього включаються вершина за вершиною в тому порядку, в якому вони отримували постійні мітки. Першим в дерево включається корінь - вершина S .

Побудуємо дерево найкоротших шляхів для нашого прикладу.

Спочатку включаємо в дерево корінь - вершину 1. Потім в дерево включається дуга (1,6). Наступною була впорядкована вершина 9, довжина найкоротшого шляху до якої дорівнює 3. Перший раз число 3 з'явилося в третьому рядку, яка заповнювалася при
. Отже, вершина 6 - передостання вершина найкоротшого шляху до вершини 9. Включаємо в дерево дугу (6,9) довжини 1.

Потім було проведено упорядкування вершина 2 з довжиною найкоротшого шляху, що дорівнює 4. Це число вперше з'явилося в третьому рядку, яка заповнювалася при
. Отже, найкоротший шлях до другої вершину проходить по дузі (6,2). Включаємо в дерево дугу (6,2) довжини 2.

Далі було проведено упорядкування вершина 12,
. Перший раз число 4 з'являється в четвертому рядку, яка заповнювалася при
. У дерево включається дуга (9,12) довжини 1. Повне дерево найкоротших шляхів показано на рис. 5.

Алгоритм Дейкстри може помилятися, якщо в графі є дуги негативною довжини. Так, відшукуючи найкоротші шляхи від вершини s \u003d 1 для графа на рис. 6, алгоритм спочатку впорядкує вершину 3, потім вершину 2 і закінчить роботу. При цьому цей найкоротший шлях до вершини 3, з точки зору алгоритму Дейкстри,  це дуга (1,3) довжини 3.

Насправді, найкоротший шлях до вершини 3 складається з дуг (1,2) і (2,3), довжина цього шляху дорівнює 5 + (- 3) \u003d 2.

Через наявність дуги (2,3) негативною довжини -3 виявилися порушеними наступні базові принципи:

найближча до s вершина лежить від неї на відстані двох дуг, а не однієї;

проміжна вершина найкоротшого шляху 1-2-3 (вершина 2) лежить далі від вершини 1 (на відстані 5), ніж кінцева вершина шляху 3.

Отже, присутність дуг негативною довжини ускладнює вирішення завдання про найкоротшому шляху і вимагає використання більш складних алгоритмів, ніж алгоритм Дейкстри.

Вирішити задачу про знаходження найкоротшого шляху алгоритмом Дейкстри.
Знайти найкоротший шлях від Х0 до Х7. Граф заданий елементами вартісної матриці

Побудуємо цей граф


Почнемо з елементу Х0 і дамо йому мітку 0, розглянемо всіх його сусідів, тому що там ще немає позначок, то дамо їм відповідні довжини:


Всі сусіди Х0 розглянуті, помічаємо її і переходимо до вершини Х1. ЇЇ сусіди Х0, Х2, Х4, але Х0 позначена, не розглядаємо її. Для Х2: , Залишаємо мітку.

Для Х4: , Замінюємо мітку. Всі сусіди вершини Х1 розглянуті, помічаємо її


переходимо до вершини Х2. ЇЇ сусіди Х0, Х1, Х3, Х4, Х5, Х6, але Х0, Х1 помічені, не розглядаємо їх.
Для Х3: , Залишаємо мітку.
Для Х5: , Замінюємо мітку.
Для Х4: , Залишаємо мітку.
Для Х6: , Замінюємо мітку.
Всі сусіди вершини Х2 розглянуті, помічаємо її.


переходимо до вершини Х3. ЇЇ сусіди Х0, Х2, Х6, але Х0, Х2 помічені, не розглядаємо їх.
Для Х6: , Залишаємо мітку.
Всі сусіди вершини Х3 розглянуті, помічаємо її.


переходимо до вершини Х4. ЇЇ сусіди Х1, Х2, Х5, Х7, але Х1, Х2 помічені, не розглядаємо їх.
Для Х5: , Замінюємо мітку.
Для Х7: , Замінюємо мітку.
Всі сусіди вершини Х4 розглянуті, помічаємо її.


переходимо до вершини Х5. ЇЇ сусіди Х2, Х4, Х6, Х7, але Х2, Х4 помічені, не розглядаємо їх.
Для Х6: , Залишаємо мітку.
Для Х7: , Залишаємо мітку.
Всі сусіди вершини Х5 розглянуті, помічаємо її.


переходимо до вершини Х6. ЇЇ сусіди Х2, Х3, Х5, Х7, але Х2, Х3, Х5 помічені, не розглядаємо їх.
Для Х7: , Залишаємо мітку.
Всі сусіди вершини Х6 розглянуті, помічаємо її. І помічаємо, що залишилася Х7, все вершини розглянуті.


Висновок: Найкоротший шлях їх Х0 в Х7 має довжину 101, цей шлях: Х7-Х4-Х1-Х0.