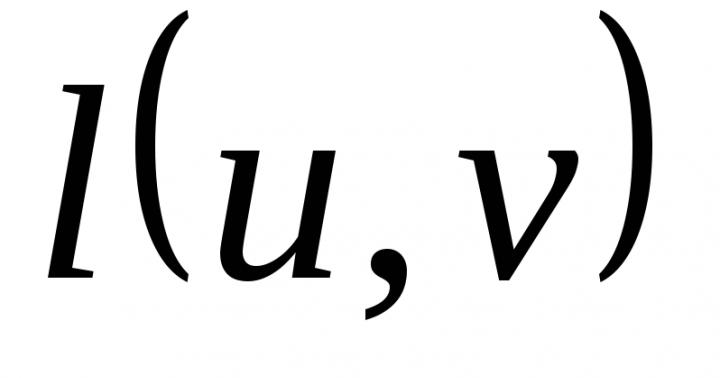The Algorithm Daekstra is an algorithm on the graphs, which finds the shortest path between the two vertices in the graph with non-negative lengths of the arc. It is also often a task of calculating the shortest path from this vertex to all others. The algorithm is widely used in programming, for example, it is used by routing protocols.
Description
The algorithm input is given a weighted oriented graph with non-negative weight arcs. The output is a set of shortest paths from this vertex to others.
At the beginning, the distance for the initial vertex is assumed to be zero, and the distances to all others are understood infinite. An array of flags denoting whether the top is passed, filled with zeros. Then, at each step of the cycle, a top with a minimum distance to the initial and flag equal to zero is searched. For it, the flag is installed and all neighboring vertices are checked. If the previous distance from the source vertex is previously checked than the amount of the distance to the current vertex and the length of the rib from it to the checked vertex, then the distance to the tested vertex equates to the distance to the current + edge from the current to the currently checked. The cycle is completed when the flags of all vertices become equal to 1, or when the distance to all vertices with flag 0 is infinite. The last case is possible then and only if the count is intolerant.
Algorithm Daekstra in pseudocode
Entrance: FROM : Array of Real - Count Arc Log Matrix; S is a vertex from which the shortest path and T is a vertex to which it is looking for.
Output: V\u003e Array of Real; and N: Array of 0..R. If the top v. Lies in the shortest path from s. to t, that T [V]- Length of the shortest path from s. to y; H [y] - Top, directly preceding w. In the shortest path.
H is an array in which the vertex n corresponds to the vertex M, the previous one on the way to n from s.
T is an array in which the vertex n corresponds to the distance from it to s.
X is an array in which the vertex n corresponds to 1 if the path is known to it, and 0, if not.
initialization of arrays:
for v. from 1 to. r do.
T [v.]: = ∞ (the shortest path is unknown)
X [v]: \u003d 0 (all vertices are not marked)
H [s]: \u003d 0 ( s. nothing precedes)
T [S]: \u003d 0 (the shortest path has a length of 0 ...)
X [s]: \u003d 1 (... and he is known) v. : = s. (current vertex)
M: (update marks)
for and ∈ G ( and) do.
if X [and] = 0 & T [and]> T [V] + C. Then.
T [and]: = T [V] + C. (a shorter path from s. in and through v. }
H [U]:= v. (remember it)
m.: = ∞
v. : = 0
(search for the end of the shortest path)
for and from 1 to. p. do.
if X [U] = 0 & T [U]< t. Then.
v:= u.;
m:= T [U] (Top v. finishes the shortest path from s.
if v. = 0 Then.
sTOP (no path from s. in t.) End if
if v.= t. Then.
stop (the shortest path from s. in t.) End if
X [v]: \u003d 1 (the shortest path from s. in v. ) Goto. M.
Justification
To prove the correctness of the Daekstra algorithm, it is enough to note that with each performance of the body of the cycle, which starts the label M, as v.a vertex is used for which the shortest path from the top is known. s.In other words, if x [v] \u003d 1, then T [v] \u003d D (S, V) , And all the vertices on the path (S, V), determined by the n vector, have the same property, that is
Vu T [and] \u003d 1 \u003d\u003e T [and] \u003d D (S, U) & T] \u003d 1.
Really (by induction), first time as v. The vertex S is used for which the shortest path is empty and has a length of 0 (non-empty paths cannot be shorter, because the length of the arcs are non-negative). Let T [U] \u003d D (S, U) for all previously marked vertices and. Consider the newly marked vertex v.which is selected from the condition T [V] \u003d MIN T [and]. Note that if the way is known through the marked vertices, then it is also known for the shortest path. Suppose (otherwise), that T [V]\u003e D (S, V), that is, the path found leading from s.in v,is not the shortest. Then there should be unremarkable vertices on this path. Consider the first vertex w.on this path, such that t [w] = 0. Iim: T [w] = d (S, W) ⩽D (S\u003e V)< Т[v],что противоречит выбору вершины u.
Temporary difficulty
The complexity of the Daekstra algorithm depends on the method of finding not visited by the top with a minimum distance to the initial, method of storing a plurality of unwitted vertices and methods of updating tags. Let N be the number of vertices, and through M - the number of edges in the column. Then, in the simplest case, when all set vertices are viewed to search the vertices with a minimum distance to the initial vertex, and an array is used to store the distances, the time of operation of the algorithm - O (N 2). The main cycle is performed about N times, in each of them, the minimum is spent about N operations. The number of operations are spent on the cycles along the neighbors of each visit the vertex, the number of ROBER M (since each edge is found in these cycles smoothly twice and requires a constant number of operations). Thus, the overall operation time of the O (n 2 + m) algorithm, but since M is less than N (N-1), ultimately it turns out about (N 2).
For rarefied graphs (that is, such for which M is much less than N²) unwitted vertices can be stored in a binary heap, and as a key to use distances. Since the cycle is performed about n times, and the number of relaxation (changes of labels) is not more than M, the time of operation of such an implementation - O (NLOGN + MLOGN)
Example
Calculation of distances from the vertex 1 for passable vertices:
Before each city area (if you can only move on the roads).
Option 2. There are some flights between cities in the world, for each famous cost. The cost of the flight from A to B may not be equal to the cost of the flight from B to A. Find the route of the minimum cost (possibly with transfers) from Copenhagen to Barnaul.
Formal definition
Example
Consider the execution of the algorithm on the example of the graph shown in the figure.
Let it be required to find the shortest distance from the 1st vertex to all others.
Implementation in programming languages
Performance in Language C (SI)
#Define Size 6 #Define INF 1000000000 INT A [SIZE] [SIZE] \u003d ((INF, 5, INF, INF, INF, INF), (1, 2, 3, 4, 5, 6), // Matrix paths (1, 2, 3, 4, 5, 6), (1, 2, 3, 4, 5, 6), // horizontal indexes from the point { 1 , 2 , 3 , 4 , 5 , 6 },{ 1 , 2 , 3 , 4 , 5 , 6 }}; // vertical to point, value - weight INT D [Size]; // Array of the shortest paths found, indexes - vertices of the graph void deikstra () (int v [size]; // array of labels int temp, i; int minindex, min; for (i \u003d 0; i< SIZE ; i ++ ) { d [ i ] = INF ; // Array of paths is initialized infinity v [i] \u003d 1; ) d [0] \u003d 0; do ( // Execution of the algorithm minindex \u003d inf; MIN \u003d INF; for (i \u003d 0; i< SIZE ; i ++ ) { if ((v [ i ] == 1 ) && (d [ i ] < min )) { min = d [ i ]; minindex = i ; } } if (minindex != INF ) { for (i = 0 ; i < SIZE ; i ++ ) { if (a [ minindex ][ i ] > 0) (temp \u003d min + a [minindex] [i]; if (Temp< d [ i ]) d [ i ] = temp ; } } v [ minindex ] = 0 ; } } while (minindex < INF ); }
shortest path Today it is a vital task and is used almost everywhere, ranging from finding the optimal route between two objects on the ground (for example, the shortest path from home to the university), in autopilot systems, to find the optimal route during transportation, switching information package in networks and T.P.The shortest path is considered using a certain mathematical object called graph. Search shortest path It is conducted between two specified vertices in the graph. The result is the path, that is, the sequence of vertices and ribs, incident to the two neighboring vertices, and its length.
Consider three most effective algorithm Laying shortest path:
- algorithm Daekstra;
- Floyd algorithm;
- overborn algorithms.
These algorithms are easily performed with a small number of vertices in the graph. With an increase in their number of search task shortest path Complete.
Algorithm Daekstra
This algorithm is an algorithm on the graphs, which was invented by the Netherlands scientist E. Dyakstroy in 1959. The algorithm finds the shortest distance from one of the vertices of the graph to all other and works only for graphs without ribs of negative weight.
Each vertex is attributed to the weight - this is the weight of the path from the initial vertex to this. Also, each vertex can be highlighted. If the vertex is highlighted, the path from it to the initial vertex the shortest, if not, then temporary. Coming by the graph, the algorithm considers the route for each vertex, and, if it turns out to be the shortest, highlights the top. Weight of this vertex is the weight of the path. For all neighbors of this vertex, the algorithm also calculates the weight, with no circumstances using them under any circumstances. The algorithm finishes its work, reaching the final vertex, and weighing shortest path The weight of the final vertex becomes.
Algorithm Daekstra
Step 1. To all tops, except for the first, the weight is assigned an equal infinity, and the first vertex is 0.
Step 2. All vertices are not highlighted.
Step 3. The first vertex is declared current.
Step 4. The weight of all unrequidated vertices is translated by the formula: the weight of the unsecined vertex is the minimum number of the old weight of this vertex, the amount of the weight of the current vertex and the weight of the edge connecting the current vertex with the undefidant.
Step 5. Among the unsecined peaks is a top with minimal weight. If this is not found, that is, the weight of all vertices is equal to infinity, the route does not exist. Consequently, the exit. Otherwise, the current is the resulting top. It is allocated.
Step 6. If the current vertex turns out to be the final, the path is found, and its weight is the weight of the final vertex.
Step 7. Go to step 4.
In software implementation algorithm Daekstra We will construct a set of s vertices for which the shortest paths from the initial vertex are already known. At each step to the set S, the same vertex is added, the distance from the initial vertex is less than for other remaining vertices. In this case, we will use the array D, in which the lengths are recorded shortest paths For each vertex. When the set S contains all the vertices of the graph, then the array D will contain lengths shortest paths From the initial vertex to each vertex.
In addition to the specified arrays, we will use the C matrix of C, where the element C is the length of the edges (i, j), if there is no ribs, then its length is relied on equal infinity, that is, more than any actual rib length. Actually matrix C is sailing matrixin which all zero elements are replaced with infinity.
To determine the itself
5.4.3. The challenge of the shortest path and the Daekster algorithm of its decision
Let the orgraf set G.(V.,
E.), with each arc of which is put in line with the number 
called arc Long.
Definition. Lena The path is called the sum of the arc lengths that make up this path. The task of the shortest pathputs like that.
Option 1. Find the lengths of the shortest paths (ways of minimal length) and the paths themselves from the fixed vertex s. to all other vertices of the graph.
Option 2. Find the lengths of the shortest paths and the paths themselves between all pairs of the vertices of this graph.
If there are negative arcs in the column, the task may not have solutions (will lose the meaning). This is due to the fact that the contour of the negative length may be present in the column. The presence of negative length circuits means that the path length can be made equal 
. And if there is no negative length circuits, then the shortest paths exist and any shortest path is a simple chain.
Note that if the shortest path exists, then any of it is, it is also the shortest path between the respective vertices.
Algorithm Daekstra solving the problem of the shortest path.
The algorithm works with arcs of positive length and defines the shortest paths from the fixed vertex s. to all other vertices of the graph. Denote these vertices v. 1 , v. 2 ,…, v. n. .
Definition. Let's call the top u. lying closer to the top s.than top v.if the length of the shortest path from s. before u. less than the length of the shortest path from s. before v.. We will say that the tops u. and v. equalued from the top s.if the lengths of the shortest paths from s. before u. and from s. before v. match up.
The Daekstra algorithm consistently streamlines the vertices of the graph in the sense of proximity to the top s. and based on the following basic principles.
If the lengths of the arc are positive numbers, then
nearest K. s. top - she herself. Length of the shortest path from s. before s. equal to 0;
nearest K. s. vertex s., Lies from s. At the distance of one arc the shortest of all arches leaving the top s.;
any intermediate top of the shortest path from s. To some vertices v. Lies closer to K. s.than final vertex v.;
the shortest path to the next ordered vertex can only pass through already ordered peaks.
Let the algorithm already ordered the peaks v. 1 ,
v. 2 …
v. k. .
Denote by 
,
The length of the shortest path to the top v. i. .
Consider all arcs of the source graph that begin in one of the vertices of the set. 
And ends in another unordered vertices. For each such arc, for example 
, I calculate the sum 
. This amount is equal to the length of the path from s.
in y.in which the vertex v. i. There is a penultimate top, and the path from s.
in v. i. - the shortest of all paths connecting s.
and v. i. .
This is the most defined lengths of all paths from s. not yet ordered peaks in which only vertices are intermediate vertices are k. Nearest K. s.. Let the shortest of these paths ends on top w.. Then w. and is 
By proximity to K. s. vertex.
Technically actions on the Daekstra algorithm are carried out using the vertex marking apparatus. Tag verth v. denotes how 
. Any label is a number equal to the length of some path from s.
before v.. Tags are divided into temporary and constant. At every step, only one label becomes constant. This means that its value is equal to the length of the shortest path to the corresponding vertex, and this vertex itself is ordered. The number of the next ordered vertex is denoted by the letter r.
Description of the algorithm.
Step 1. (Initial installation). Put 
And consider this label constant. Put 
,
And consider these marks temporary. Put 
.
Step 2. (Shared step). He repeats n. once all the vertices of the graph are ordered.
Recalculate a temporary mark 
All disordered vertices v. i. which includes an arc leaving the top r, By rule
Select top with a minimum time label. If there are several such vertices, choose any.
Let be w.-
Top with a minimum time label. Take a label 
constant and put 
.
The steps of the Daekstra algorithm are conveniently drawn up in the table, each column of which corresponds to the vertex of the graph. The rows of the table correspond to the repetition of the overall step.
Example.
For graph in Fig. 4. Find the shortest paths from the vertices 
to all other vertices of the graph. Ribs mean two multi-directional arcs of the same length.
Decision. In tab. 1 recorded vertex tags at every step. Permanent tags are marked with "+". Let us describe in detail how the tags are calculated.
From the vertex 1 arcs are overlooking the vertices 2, 5, 6. Recalling the labels of these vertices and fill the second string of the table.
Top of the vertex 6 becomes constant, 
.
From the vertex 6 arcs are still unordered vertices 2, 5, 8, 9. Recalculate their time tags
Fill 3 rows of table. The minimum of the time labels is 3 (Top Tag 9), 
.
From the vertex 9 arcs in still unordered vertices 5, 8, 11, 12. Then
Fill the fourth line of the table. In this line, two vertices 2 and 12 have minimal time tags equal to 4. First order, for example, the vertex 2. Then the top 12 will be ordered at the next step.
Table 1
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
.
From the top 2 there are arcs in still disordered vertices 3, 4, 5. Recalling temporary marks of these vertices
Fill out 5 table rows. The minimum of time labels is 4 (vertex tag 12), 
.
Fill 6 rows of table. The minimum of time labels is 5 (Top Tag 5), 
.
Fill 7 string of the table. Become a constant tag of the vertex 8 (it is equal to 5), 
.
Top 11 is ordered.
From the vertex 11 arcs in disordered vertices 7, 10. Recalling the time marks of these vertices.
Top 4 gets a constant tag.
From the vertex 4 arcs in unordered vertices 3, 7. Recalculate time tags
Organize the vertex 3.
Fill 12 table rows. At this step, we order the last disordered vertex 10.
Building a tree of shortest paths.
The Tree of the shortest paths is a focused tree with a root in the top S. . All paths in this tree are the shortest for this graph.
The shortest path tree is based on the table, the top is turned on over the vertex in the order in which they received constant tags. The first in the tree turns on the root - the vertex S. .
We construct the shortest way tree for our example.
First, we turn on the root in the tree - the vertex 1. Then the arc is turned into a tree (1.6). The next one was ordered the vertex 9, the length of the shortest path to which is equal to 3. The first time number 3 appeared in the third line, which was filled with 
. Consequently, the vertex 6 is the penultimate top of the shortest path to the vertex 9. We turn in the wood arc (6.9) length 1.
The top 2 was ordered with the length of the shortest path equal to 4. This number for the first time appeared in the third line, which was filled with 
. Consequently, the shortest path in the second vertex passes along the arc (6.2). We turn on the arc (6.2) of length 2.
Next was ordered the top 12, 
. The first time number 4 appears in the fourth line, which was filled with 
. The tree includes an arc (9.12) of length 1. The total tree of the shortest paths is shown in Fig. five.
The deiquist algorithm can be wrong if there are negative arcs in the column. So, looking for the shortest paths from the top s. \u003d 1 for graph in fig. 6, the algorithm first ordered the vertex 3, then the vertex 2 and finish the work. In this case, this shortest path to the top 3, from the point of view of the Daekstra algorithm, is an arc (1.3) length 3.
In fact, the shortest path to the vertex 3 consists of arcs (1.2) and (2.3), the length of this path is 5 + (- 3) \u003d 2.
Due to the presence of an arc (2.3) of a negative length -3, the following basic principles were disturbed:
nearest K. s. The peak lies from it at a distance of two arcs, and not one;
the intermediate top of the shortest path 1-2-3 (vertex 2) lies further from the vertex 1 (at a distance of 5) than the final vertex of the path 3.
Consequently, the presence of negative length arc complicates the solution of the problem of the shortest path and requires the use of more complex algorithms, rather than the Daekstra algorithm.
Solve the task of finding the shortest path of the Daekstra algorithm.
Find the shortest path from x0 to x7. Count is set by the elements of the cost matrix
Build this graph 
Let's start with the element x0 and we assign it a tag 0, consider all his neighbors, because There is still no note, you assign them the corresponding lengths: 
All neighbors x0 are considered, we mark it and go to the top of X1. Its neighbors x0, x2, x4, but x0 marked, do not consider it. For x2: 
, Leave the label.
For x4: 
Replacing the label. All neighbors of the vertex X1 are considered, we mark it 
Go to the top of X2. Its neighbors x0, x1, x3, x4, x5, x6, but x0, x1 are marked, do not consider them.
For x3: 
, Leave the label.
For x5: 
Replacing the label.
For x4: 
, Leave the label.
For x6: 
Replacing the label.
All neighbors of the top of the X2 are considered, we mark it. 
Go to the top x3. Its neighbors x0, x2, x6, but x0, x2 are marked, do not consider them.
For x6: 
, Leave the label.
All neighbors of the top of the X3 are considered, we mark it. 
Go to the top of X4. Its neighbors x1, x2, x5, x7, but x1, x2 are marked, do not consider them.
For x5: 
Replacing the label.
For x7: 
Replacing the label.
All neighbors of the top of the X4 are considered, we mark it. 
Go to the top of X5. Its neighbors x2, x4, x6, x7, but x2, x4 are marked, do not consider them.
For x6: 
, Leave the label.
For x7: 
, Leave the label.
All neighbors of the top of the X5 are considered, we mark it. 
Go to the top of x6. Its neighbors x2, x3, x5, x7, but x2, x3, x5 are marked, do not consider them.
For x7: 
, Leave the label.
All tops of the top of the X6 are considered, we mark it. And we labeled the remaining x7, all the vertices are considered. 
Conclusion: The shortest path of their x0 in x7 has a length of 101, this path: x7-x4-x1-x0.
